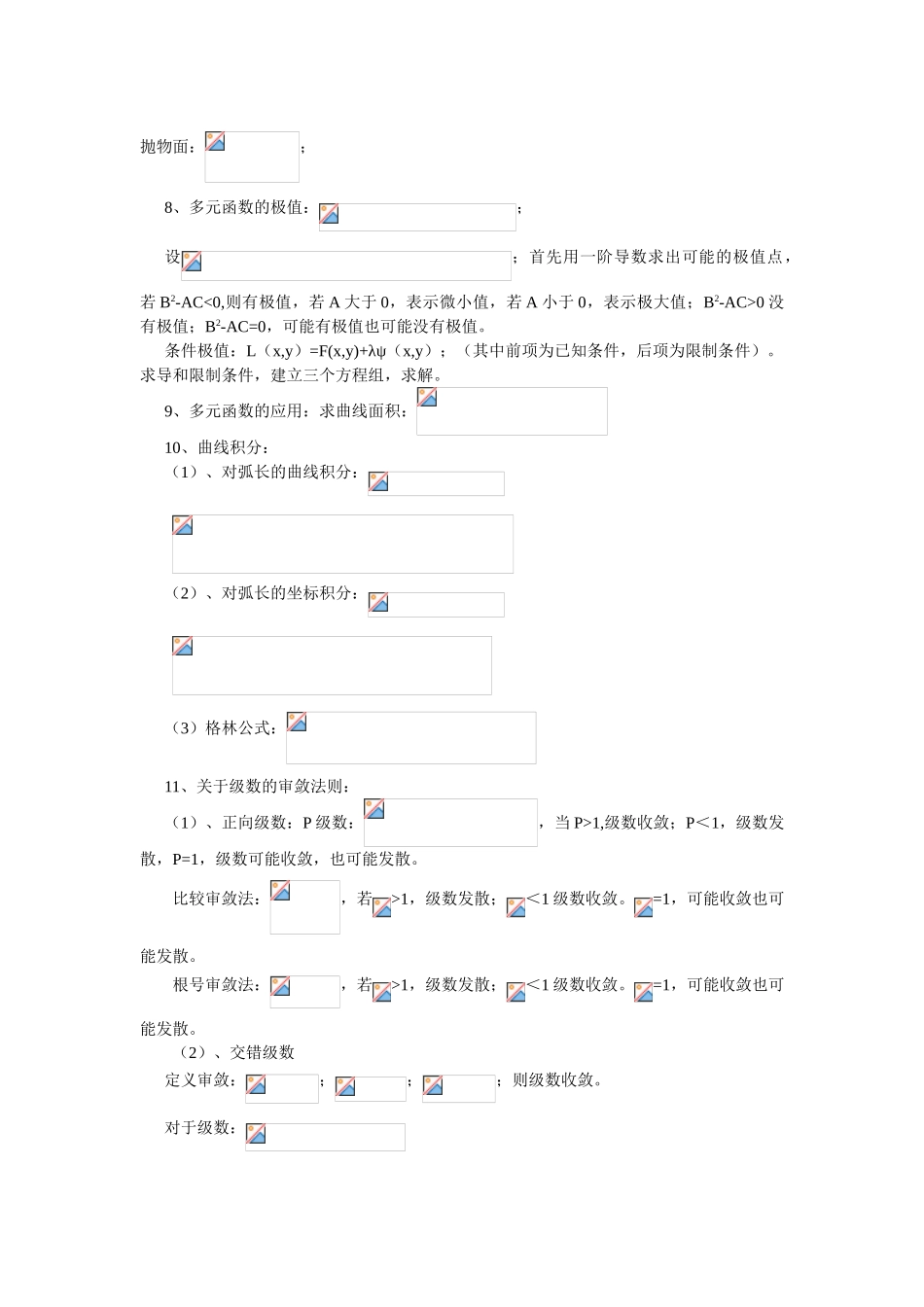
高等数学1 、 双 曲 正 弦 曲 线 :; 双 曲 余 弦 :; 双 曲 正 切 :;双曲余切:2、极限的定义表示方法:3、两个函数的重要准则:;4、函数的间断点:第一类间断点:(两边极限都存在且相等:可去间断点;两边极限都存在,不相等为跳跃间断点。第二类间断点:极限不存在或震荡间断点。5、关于函数的求导法则:一:隐函数的求导法则:;参数函数的求导法则: ;;6、关于二元函数的极值、单调性、凸凹性、拐点问题:关于二元函数的单调性:表示函数递增;小于 0,表示函数递减;表示函数凹,小于 0,表示函数凸。函数的二阶导数为 0,表示函数为拐点;求函数极值的办法为:首先找出驻点(一阶导数为 0 的点或导数不存在的点,判定两边的一阶导数是否变号,若左边小于 0,右边大于 0,则表示为最小值;左边大于 0,右边小于 0,则表示为最大值。若二阶导数不为 0,大于 0,则有最小值,小于 0,这有最大值。7、关于几个二次曲线、曲面:(1)双曲线:,若绕 Z 轴旋转:旋转单页双曲面:绕 X 轴旋转:,旋转双叶双曲面。(2)椭圆锥面:;椭圆球面:;单叶双曲面:;双叶双曲面:;椭圆抛物面:;双曲抛物面:;8、多元函数的极值:;设;首先用一阶导数求出可能的极值点,若 B2-AC<0,则有极值,若 A 大于 0,表示微小值,若 A 小于 0,表示极大值;B2-AC>0 没有极值;B2-AC=0,可能有极值也可能没有极值。条件极值:L(x,y)=F(x,y)+λψ(x,y);(其中前项为已知条件,后项为限制条件)。求导和限制条件,建立三个方程组,求解。9、多元函数的应用:求曲线面积:10、曲线积分:(1)、对弧长的曲线积分:(2)、对弧长的坐标积分:(3)格林公式:11、关于级数的审敛法则:(1)、正向级数:P 级数:,当 P>1,级数收敛;P<1,级数发散,P=1,级数可能收敛,也可能发散。比较审敛法:,若>1,级数发散;<1 级数收敛。=1,可能收敛也可能发散。根号审敛法:,若>1,级数发散;<1 级数收敛。=1,可能收敛也可能发散。(2)、交错级数定义审敛:;;;则级数收敛。对于级数:若:收敛则绝对收敛;若收敛,而发散则条件收敛。12、关于函数的展开:(1)公式一:(2)特别级数:其中:;对于奇函数:只有 bn;对于偶函数有 a0,an;对于函数的收敛:若连续则收敛于 f(x),若不连续,收敛于(f(x 左)+f(x 右))/213、关于微分方程的特征根问题:特征根:;若:p2-4q>0,则有两个不等实根,则...