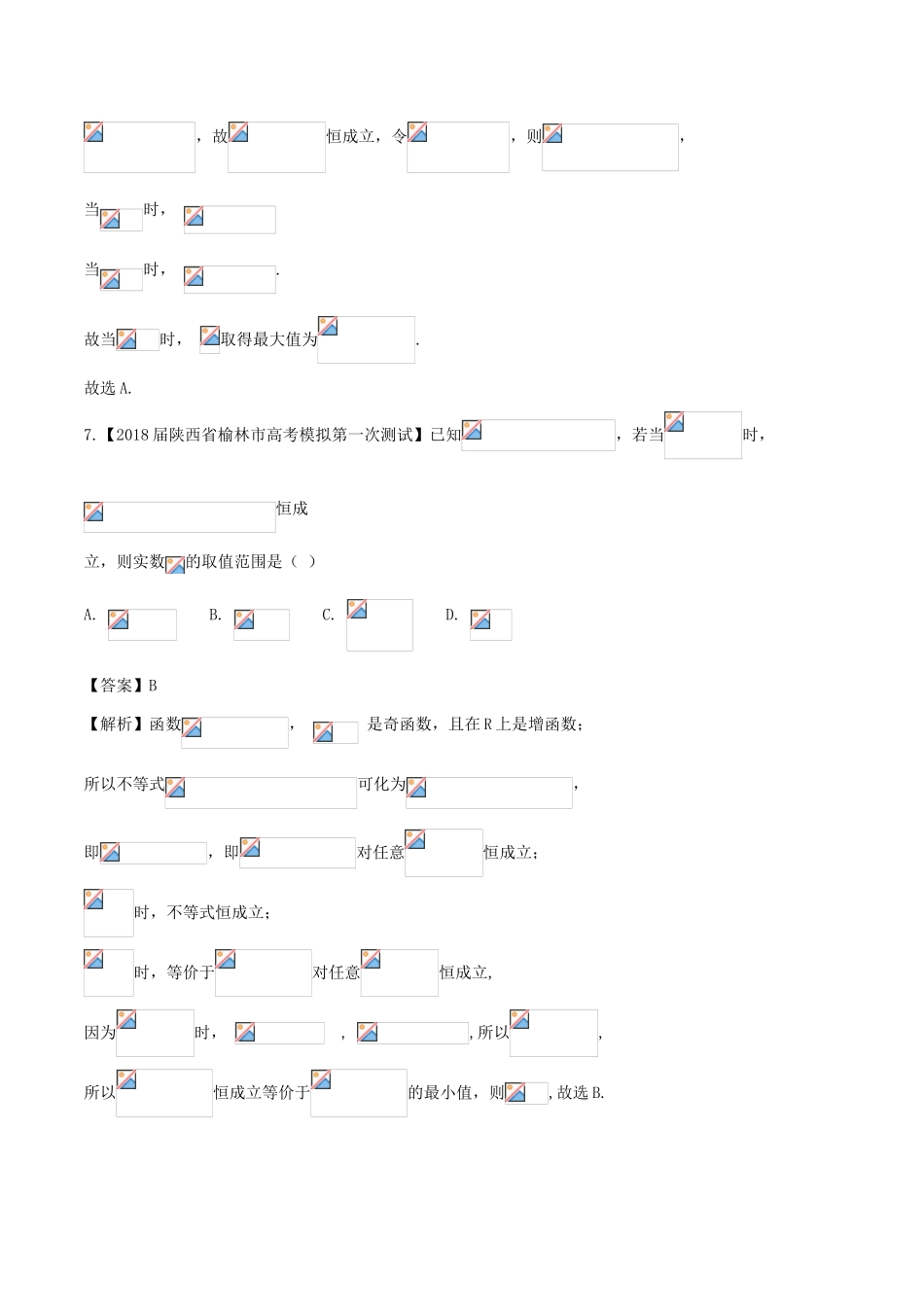
方法四分离(常数)参数法总分_______时间_______班级_______学号_______得分_______(一)选择题(12*5=60分)1.【2018届海南省高三二模】已知为锐角,,则的取值范围为()A.B.C.D.【答案】C2.当时,不等式恒成立,则实数的取值范围是()A.(-∞,3]B.[3,+∞)C.[,+∞)D.(-∞,]【答案】D【解析】因为当时,不等式恒成立,所以有,记,设,则在上是增函数,所以得,故选D.3.已知函数,若当时,恒成立,则实数的取值范围是()A.B.C.D.【答案】D【解析】是奇函数,单调递增,所以,得,所以,所以,故选D。4.若不等式恒成立,则实数a的取值范围是()A.(-∞,0)B.(-∞,4]C.(0,+∞)D.[4,+∞)【答案】B.5.若存在正数使成立,则的取值范围是()A.B.C.D.【答案】B【解析】因为,故,,记,则单调递增,所以,若存在正数使成立,则的取值范围是.6.已知等比数列的前项和为,且,若对任意的,恒成立,则实数的取值范围为()A.B.C.D.【答案】A【解析】由题意知,解得,,故恒成立,令,则,当时,当时,.故当时,取得最大值为.故选A.7.【2018届陕西省榆林市高考模拟第一次测试】已知,若当时,恒成立,则实数的取值范围是()A.B.C.D.【答案】B【解析】函数,是奇函数,且在R上是增函数;所以不等式可化为,即,即对任意恒成立;时,不等式恒成立;时,等价于对任意恒成立,因为时,,,所以,所以恒成立等价于的最小值,则,故选B.8.【2018届高三训练题】若不等式对恒成立,则实数的取值范围是()A.B.C.D.【答案】B【解析】不等式对恒成立,即不等式对恒成立,只需在内的图象在图象的下方即可,当时,显然不成立;当时,在同一坐标系中作出函数和函数的图象(如图所示),则,即,所以;故选B.9.【2016届高三山西省大同市调研】已知函数是定义在上的奇函数,当时,,若,,则实数的取值范围为()A.B.C.D.【答案】B10.设函数,对于满足的一切值都有,则实数的取值范围为()A.B.C.D.【答案】D【解析】满足的一切值,都有恒成立,可知,满足的一切值恒成立,,,实数的取值范围是,实数的取值范围为,故选D.11.定义在上的函数对任意都有,且函数的图象关于(1,0)成中心对称,若满足不等式,则当时,的取值范围是()A.B.C.D.【答案】D【解析】设,则.由,知,即,所以函数为减函数.因为函数的图象关于成中心对称,所以为奇函数,所以,所以,即.因为,而在条件下,易求得,所以,所以,所以,即,故选D.12.现有两个命题:(1)若,且不等式恒成立,则的取值范围是集合;(2)若函数,的图像与函数的图像没有交点,则的取值范围是集合;则以下集合关系正确的是()A.B.C.D.【答案】C【解析】对(1):由得即.不等式恒成立,等价于恒成立.这只需即可.(当时,取等号).的取值范围是.(1)填空题(4*5=20分)13.已知函数,若在区间上是增函数,则实数的取值范围______.【答案】.【解析】 在恒成立,即在恒成立, ,∴,即.14.【2018届福建省仙游金石中学高三上学期期中】当时,不等式恒成立,则实数的取值范围是__________.【答案】【解析】当时,不等式恒成立等价于:当时,恒成立又∴故答案为:15.设是定义在上的奇函数,且当时,,若对任意的,不等式恒成立,则实数的取值范围是.【答案】.【解析】 是定义在上的奇函数,且当时,,∴当,有,,∴,即,∴,∴在上是单调递增函数,且满足, 不等式在恒成立,∴在恒成立,解得在恒成立,∴,解得:,则实数的取值范围是.16.【2018届上海市长宁、嘉定区高三第一次质量调研(一模)】若不等式对任意满足的实数,恒成立,则实数的最大值为__________.【答案】【解析】 不等式x2−2y2⩽cx(y−x)对任意满足x>y>0的实数x、y恒成立,∴,令=t>1,∴,,当时,f′(t)>0,函数f(t)单调递增;当时,f′(t)<0,函数f(t)单调递减。∴当时,f(t)取得最小值,.∴实数c的最大值为.三、解答题(6*12=72分)17.【2018届河南省豫南九校高三下学期第一次联考】设正项等比数列,,且的等差中项为.(1)求数列的通项公式;(2)若,数列的前项和为,数列满足,为数列的前项和,若恒成立,求的取值范围.【答案】(1)(2)【解析】【试题分...