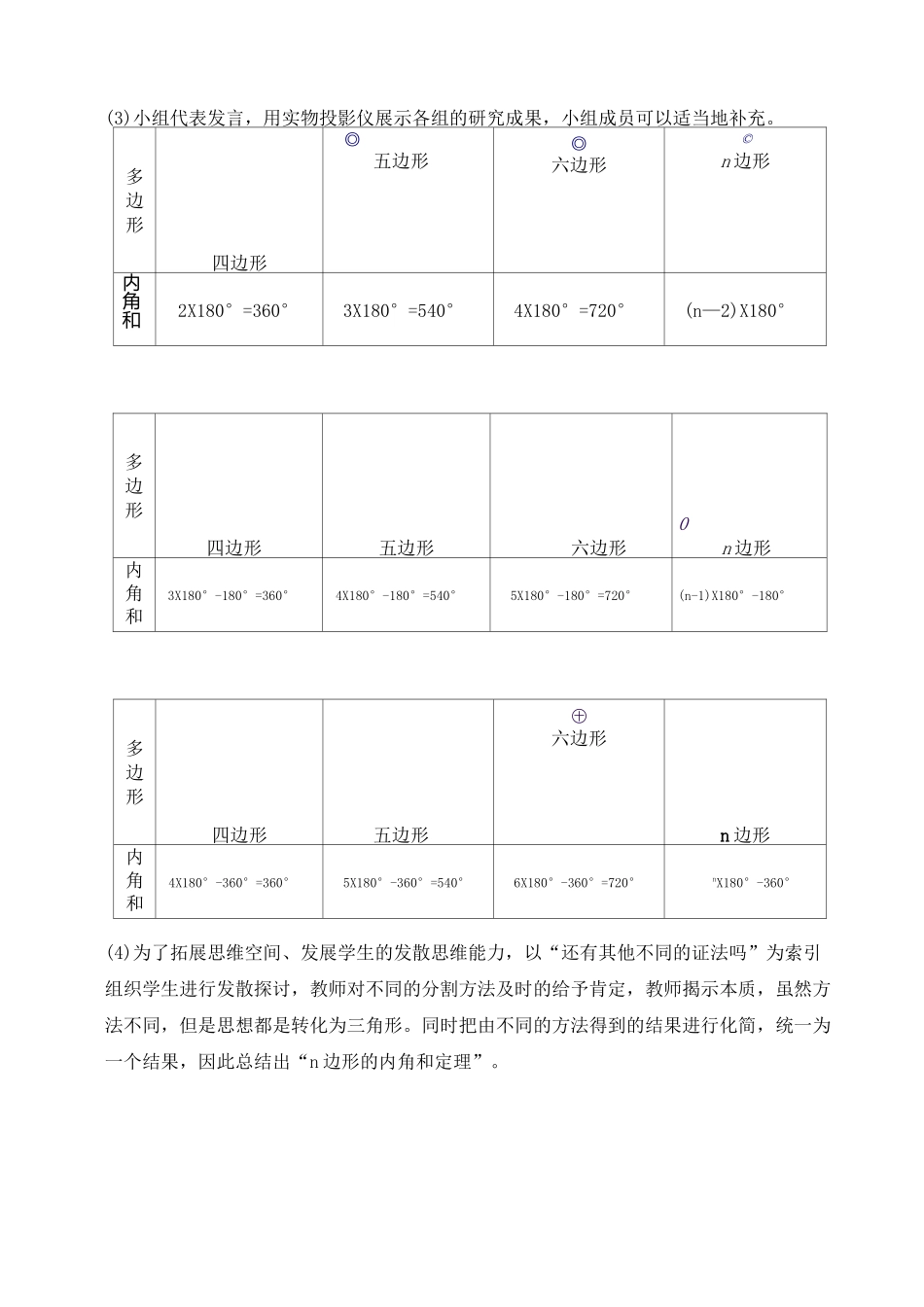
多边形内角和》教案一、教学目标1、知识技能:了解多边形内角和公式。2、数学思考:通过把多边形转化成三角形的过程,让学生体会转化思想在几何中的运用,同时也让学生体会从特殊到一般的认识问题的方法。3、解决问题:通过探索多边形内角和公式,尝试从不同角度寻求解决问题的方法并能有效地解决问题。4、情感态度目标:通过猜想、推理活动感受数学活动充满着探索以及数学结论的确定性,提高学生学习热情。二、教学重、难点重点:探索多边形内角和公式。难点:探索多边形内角和时,如何把多边形转化成三角形。三、教学方法:引导发现法、讨论法、探究法。四、教学过程:(一)情境创设,导入新课活动:出示一块彩色的三角形图片,用剪刀过边与边方式剪去一个角,再剪去一个角问题:在整个过程中,图形发生了什么变化?(活动的设计旨在让孩子们通过观察、从三角形转化为四边形、五边形的过程中体会到它们之间的联系,这将有助于后续问题的解决。同时,从孩子们的回答中寻找一个知识点来研究,因此很自然的引出课题。)(二)诱导尝试,探究新知1、以问激趣,激发求知欲(1) 大家知道三角形的内角和是多少吗?(2) 长方形、正方形的内角和又是多少?由此你能猜出一般四边形的内角和吗?(3) 五边形、六边形的内角和呢?(4) 102 边形的内角和呢?(设计意图:从孩子们已有的知识与经验出发,由已知的三角形和特殊的四边形的内角和自然过渡到对任意四边形的内角和地猜想,再展示课前通过量或拼的方法得出的五边形、六边形的内角和,让他们从操作中感受量或拼的方法的复杂性和局限性,特别是当边数较大时更难以操作,由此引发冲突,激发孩子求知欲,使孩子的思维处于愤悱状态,然后以“必须寻找出多边形内角和的规律,大家才能轻而易举地解决问题(4)”为引子很自然地进入探究新知的环节)2、验证假设,获得定论从探索四边形的内角和到五边形、六边形、乃至 n 边形,让孩子们体会由简单到复杂,由特殊到一般的思想方法,经历化归转化的过程,在这个过程中鼓励孩子探索问题,要追求多样化,同时在多样化的方法当中,要抓住解决问题的关键,揭示方法与方法之间是存在内在联系的。并鼓励孩子积极参与,合作交流,发展孩子的语言表达能力、数学推理能力和创新能力。教学过程为:(2)孩子们独立思考,前后两排四人一组分工讨论交流,教师深入小组巡视指导。(3)小组代表发言,用实物投影仪展示各组的研究成果,小组成员可以适当地补充。多边形四边形◎五边形◎...