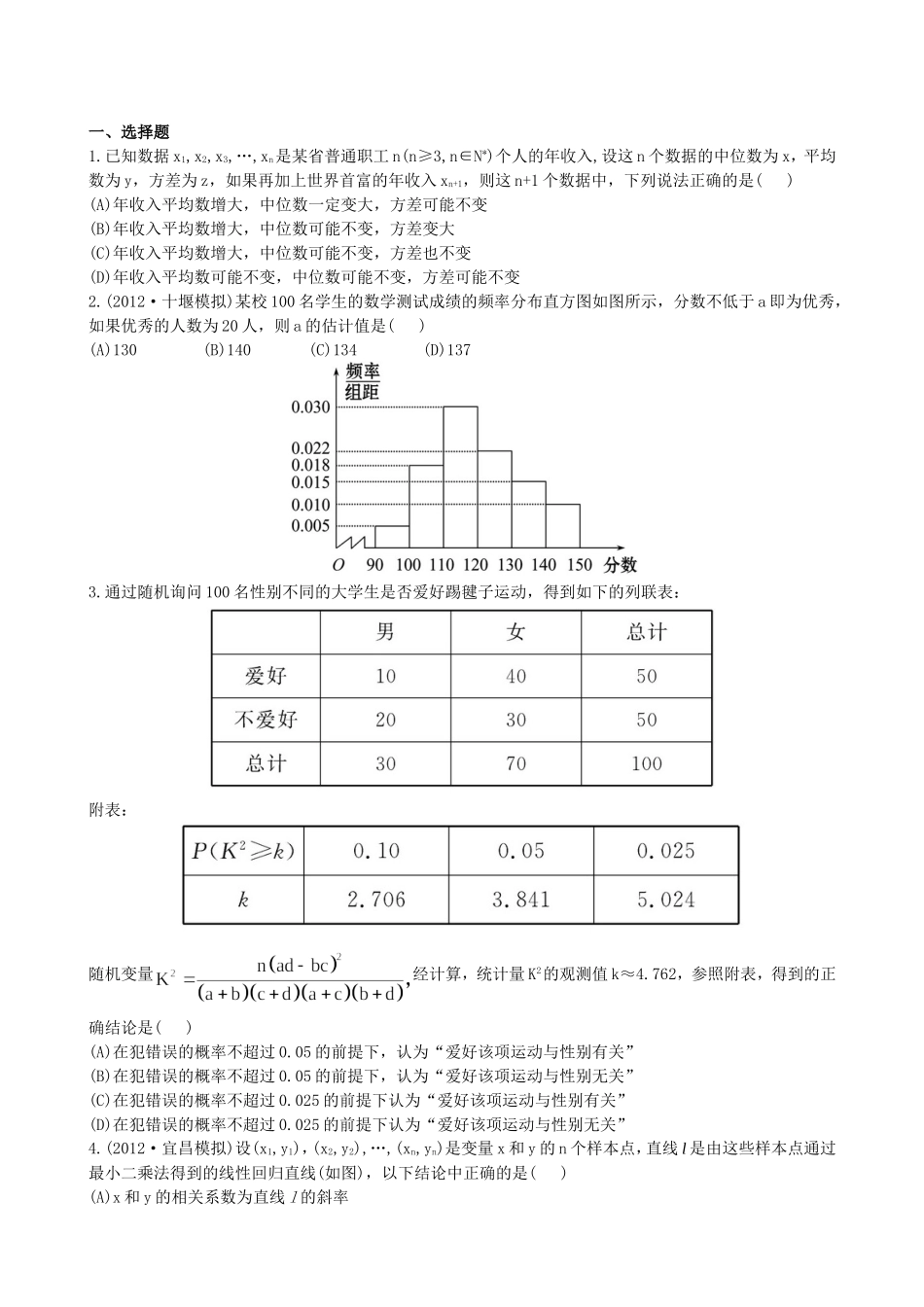
一、选择题1.已知数据x1,x2,x3,…,xn是某省普通职工n(n≥3,n∈N*)个人的年收入,设这n个数据的中位数为x,平均数为y,方差为z,如果再加上世界首富的年收入xn+1,则这n+1个数据中,下列说法正确的是()(A)年收入平均数增大,中位数一定变大,方差可能不变(B)年收入平均数增大,中位数可能不变,方差变大(C)年收入平均数增大,中位数可能不变,方差也不变(D)年收入平均数可能不变,中位数可能不变,方差可能不变2.(2012·十堰模拟)某校100名学生的数学测试成绩的频率分布直方图如图所示,分数不低于a即为优秀,如果优秀的人数为20人,则a的估计值是()(A)130(B)140(C)134(D)1373.通过随机询问100名性别不同的大学生是否爱好踢毽子运动,得到如下的列联表:附表:随机变量经计算,统计量K2的观测值k≈4.762,参照附表,得到的正确结论是()(A)在犯错误的概率不超过0.05的前提下,认为“爱好该项运动与性别有关”(B)在犯错误的概率不超过0.05的前提下,认为“爱好该项运动与性别无关”(C)在犯错误的概率不超过0.025的前提下认为“爱好该项运动与性别有关”(D)在犯错误的概率不超过0.025的前提下认为“爱好该项运动与性别无关”4.(2012·宜昌模拟)设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归直线(如图),以下结论中正确的是()(A)x和y的相关系数为直线l的斜率(B)x和y的相关系数在0到1之间(C)当n为偶数时,分布在l两侧的样本点的个数一定相同(D)直线l过点()5.已知茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为()(A)(B)(C)(D)6.(2012·江西高考)样本(x1,x2,…,xn)的平均数为样本(y1,y2,…,ym)的平均数为若样本(x1,x2,…,xn,y1,y2,…,ym)的平均数其中0<α<则n,m的大小关系为()(A)n<m(B)n>m(C)n=m(D)不能确定二、填空题7.(2012·广东高考)由正整数组成的一组数据x1,x2,x3,x4,其平均数和中位数都是2,且标准差等于1,则这组数据为________(从小到大排列).8.从某地高中男生中随机抽取100名同学,将他们的体重(单位:kg)数据绘制成如下的频率分布直方图.由图中数据可知体重的平均值为________kg;若要从体重在[60,70),[70,80),[80,90]三组内的男生中,用分层抽样的方法选取12人参加一项活动,再从这12人中选两人当正、副队长,则这两人体重不在同一组内的概率为________.9.(2012·恩施模拟)某产品的广告费用z与销售额y的统计数据如下表根据上表可得回归直线方程中的为9.4,据此模型预测广告费用为6万元时销售额为________.三、解答题10.(2012·洛阳模拟)有A,B,C,D,E五位工人参加技能竞赛培训.现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次.用茎叶图表示这两组数据如下:(1)现要从A,B中选派一人参加技能竞赛,从平均状况和方差的角度考虑,你认为派哪位工人参加合适?请说明理由;(2)若从参加培训的5位工人中选2人参加技能竞赛,求A,B两人中至少有一人参加技能竞赛的概率.11.我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准,用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了100位居民某年的月均用水量(单位:吨),制作了频率分布直方图.(1)由于某种原因,频率分布直方图部分数据丢失,请在图中将其补充完整;(2)用样本估计总体,如果希望80%的居民每月的用水量不超出标准,则月均用水量的最低标准定为多少吨,请说明理由;(3)从频率分布直方图中估计该100位居民月均用水量的平均数(同一组中的数据用该区间的中点值代表).12.(2012·北京高考)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数据统计如下表(单位:吨):(1)试估计厨余垃圾投放正确的概率;(2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”...