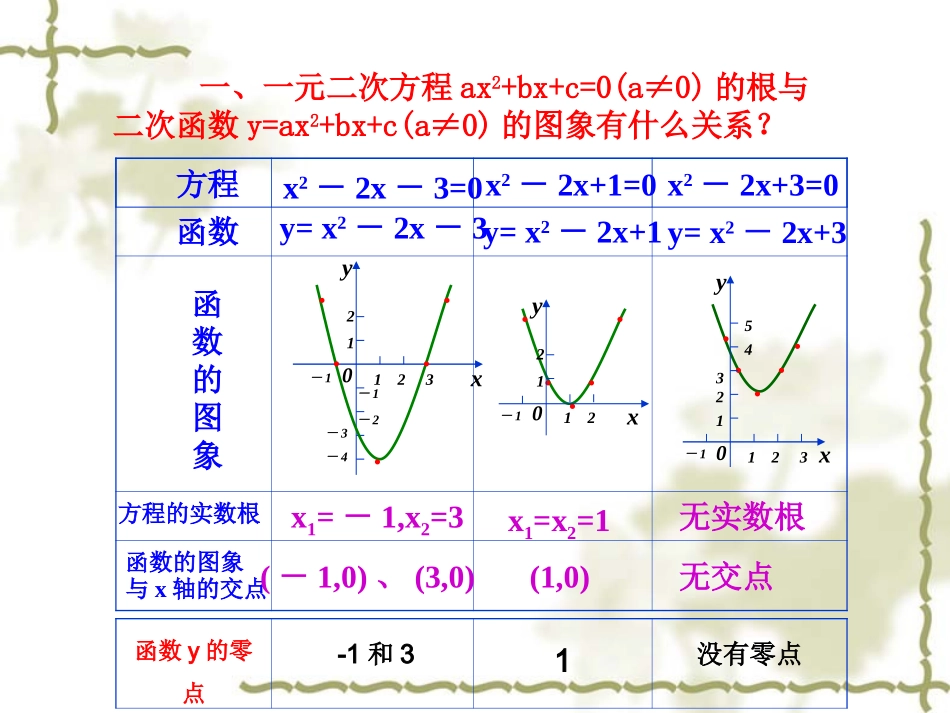
高三数学第一轮复习函数与方程第一课:方程的根与函数的零点数学组:普布顿珠说课函数零点的定义求函数的零点判断函数在区间内是否存在零点方程的根与函数的图像及函数的零点之间的关系方程x2-2x+1=0x2-2x+3=0y=x2-2x-3y=x2-2x+1函数函数的图象方程的实数根x1=-1,x2=3x1=x2=1无实数根函数的图象与x轴的交点(-1,0)、(3,0)(1,0)无交点x2-2x-3=0xy0-132112-1-2-3-4..........xy0-132112543.....yx0-12112y=x2-2x+3一、一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?函数y的零点-1和31没有零点对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。注:零点不是点,而是常数。方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点函数零点的定义:函数零点的定义:等价关系等价关系第二步:求方程f(x)=0的根第三步:方程根就是函数的零点第一步:令y=0,使f(x)=0二、如何求函数y=f(x)的零点其解题过程:例题1:求函数f(x)=x2-2x-3的零点:解:令f(x)=0,使得x2-2x-3=0(x-3)(x+1)=0-13,x解得:x21所以函数f(x)=x2-2x-3的零点分别为3和-1:练习1:求下列函数的零点(1)f(x)=2x-3(2)f(x)=x2-4(3)f(x)=-x2+3x+2三、如何判断函数在区间内是否存在零点如果函数y=f(x)在区间(a,b)上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内一定存在零点。注注::只要满足上述两个条件只要满足上述两个条件,,就能判断函数在指定就能判断函数在指定区间内存在零点。区间内存在零点。xxyy00aabb....xxyy00aabbxxyy00aabb........xxyy00aabb....如果如果f(a)·f(b)>0时,函数在区间(a,b)内不一定存在零点。例题2:已知函数f(x)=-x3-2x+5在区间(-1,2)上的图象是连续不断的一条曲线,判断函数在(-1,2)内是否存在零点解:因为函数f(x)=-x3-2x+5且x∈(-1,2)所以f(-1)=-(-1)3-2×(-1)+5=1+2+5=8>0f(2)=-(2)3-2×2+5=-8-4+5=-7<0又因为f(-1)·f(2)=8×(-7)=-56<0所以函数f(x)=-x3-2x+5在区间(-1,2)内存在零点(1)f(x)=2(1)f(x)=2x-5,x∈(-3,4)练习2:下列函数在给定区间上的图象是连续不断的一条曲线,请判断区间内是否存在零点(2)f(x)=(2)f(x)=x2-5x+8,x∈(0,1)(3)f(x)=(3)f(x)=-x2+2x-7,x∈(-1,3)小结等价关系等价关系函数零点的定义函数的零点或零点在区间内存在性的判断课后练习题已知函数f(x)=x3+x2+m在区间(-2,-1)存在零点,求m的值函数f(x)=lnx-2一定存在零点的区间是()课后思考题A.1,2B.2,31C.,1eD.3,