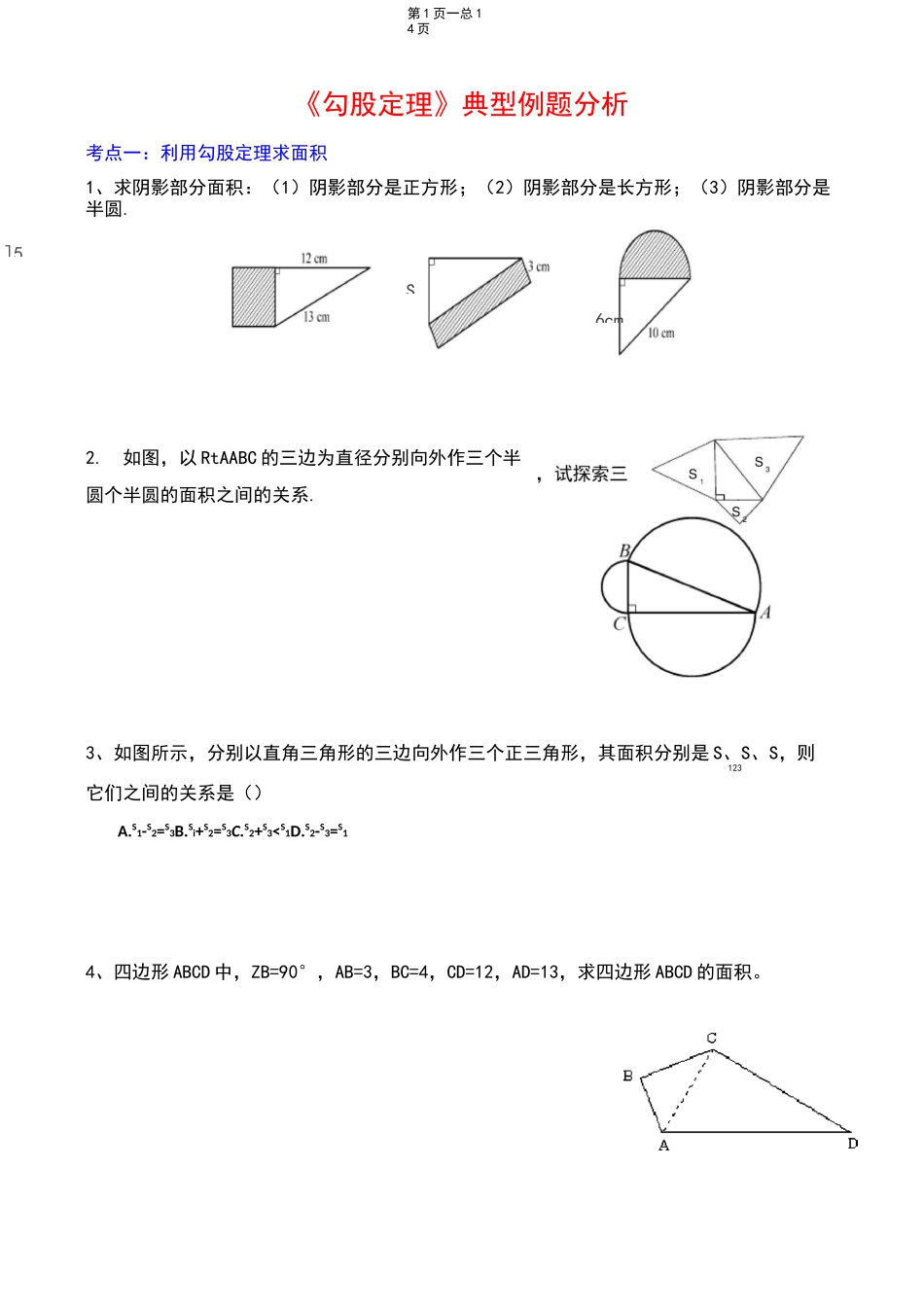
第1页一总14页《勾股定理》典型例题分析考点一:利用勾股定理求面积1、求阴影部分面积:(1)阴影部分是正方形;(2)阴影部分是长方形;(3)阴影部分是半圆.2.如图,以RtAABC的三边为直径分别向外作三个半圆个半圆的面积之间的关系.3、如图所示,分别以直角三角形的三边向外作三个正三角形,其面积分别是S、S、S,则123它们之间的关系是()A.S1-S2=S3B.Si+S2=S3C.S2+S31),那么它的斜边长是()A、2nB、n+1C、n2—1D、n2+17、在Rt^ABC中,a,b,c为三边长,则下列关系中正确的是()A.a2+b2=c2B.a2+c2=b2C.c2+b2=a2D.以上都有可能8、已知Rt^ABC中,ZC=90°,若a+b=14cm,c=10cm,则Rt^ABC的面积是()A、24cm2B、36cm2C、48cm2D、60cm29、已知x、y为正数,且丨X2-4|+(y2-3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为()A、5B、25C、7D、1510、已知在△ABC中,AB=13cm,AC=15cm,高AD=12cm,求厶ABC的周长。(提示:两种情况)考点三:应用勾股定理在等腰三角形中求底边上的高1、2、3A.4,5,6B.2,3,4若线段a,b,c组成直角三角形,A、2:3:B、3:4:面的三角形中:C.11,12,13则它们的比为(C、5:12:D8,15,1D、4:6:4、A.等腰三角C.等腰直角三角5、A.1个B.2个C.3个D.4个若三角形的三边之比为孚存1,则这个三角形一定是B直角三角D不等边三角考点四:勾股数的应用、利用勾股定理逆定理判断三角形的形状、最大、最小角的问题列各组数据中的三个数,可作为三边长构成直角三角形的是①厶ABC中,ZC二ZA—ZB;②厶ABC中,ZA:ZB:ZC=1:2:3;③AABC中,a:b:c=3:4:5;④厶ABC中,三边长分别为8,15,17.其中是直角三角形的个数有().已知a,b,。为厶ABC三边,且满足(a2—b2)(a2+b2—C2)=0,则它的形状为()A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形6、将直角三角形的三条边长同时扩大同一倍数,得到的三角形是()A.钝角三角形B.锐角三角形C.直角三角形D.等腰三角形7、若厶ABC的三边长a,b,c满足a2+b2+C2+200=12a+16b+20c,试判断AABC的形状。第3页—总14页第4页一总14页8、△ABC的两边分别为5,12,另一边为奇数,且a+b+c是3的倍数,则c应为此三角形为。例3:求(1)若三角形三条边的长分别是7,24,25,则这个三角形的最大内角是度。(2)已知三角形三边的比为1:<3:2,则其最小角为。考点五:应用勾股定理解决楼梯上铺地毯问题某楼梯的侧面视图如图3所示,其中^=4米,NMC=30°,zu=9tr,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的长度应为.E3考点六、利用列方程求线段的长(方程思想)CA第5页—总143、如图,一个长为10米的梯子,斜靠在墙面上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端下滑1米,那么,梯子底端的滑动距离1米,(填“大于”“等于”或“小于”4、在一棵树10m高的B处,有两只猴子,一只树20m处的池塘A处;□另外一只爬到树顶D处外,距离以直线计算,如果两只猴子所经过的距棵树有多高?5、如图,是一个外轮廓为矩形的机器零件平面示意图,根据图中标出尺寸(单位:mm)计算两圆孔中心A和B的距离为.爬下树走到离后直接跃到A离相等,试问6O7第5题图A.2522C.7D第6页一总14页6、如图:有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另...