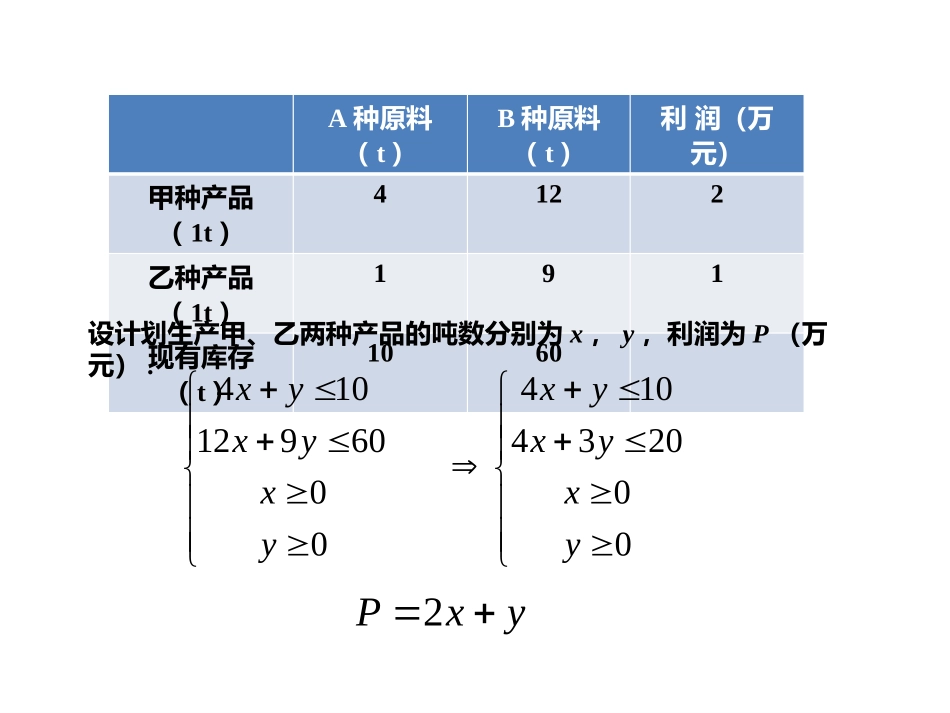
苏教版高中数学必修5第三章苏教版高中数学必修5第三章3.3.3简单的线性规划问题第1课时简单的线性规划问题课标解读1.了解目标函数、约束条件、可行域、最优解等基本概念.2.掌握线性规划问题的求解过程,特别是确定最优解的方法.(重点、难点)问题情境:我们先考察生产中遇到的一个问题:某工厂生产甲、乙两种产品,生产1t甲种产品需要A种原料4t、B种原料12t,产生的利润为2万元;生产1t乙种产品需要A种原料1t、B种原料9t,产生的利润为1万元.现有库存A种原料10t,B种原料60t,问如何安排才能使利润最大?A种原料(t)B种原料(t)利润(万元)甲种产品(1t)4122乙种产品(1t)191现有库存(t)1060设计划生产甲、乙两种产品的吨数分别为x,y,利润为P(万元).4101296000xyxyxy410432000xyxyxy2Pxy在约束条件410432000xyxyxy下,如何探求目标函数的最大值?2Pxy基础知识梳理1.线性规划中的基本概念名称意义约束条件由变量x,y组成的_________线性约束条件由x,y的一次不等式(或方程)组成的不等式组目标函数欲求最大值或最小值所涉及的变量x,y的函数解析式线性目标函数关于x,y的一次解析式不等式(组)名称意义可行解满足_________________的解(x,y)可行域所有________组成的集合最优解使目标函数取得______的可行解线性规划问题求线性目标函数在_________条件下的最大值或最小值的问题2.解决简单的线性规划问题的方法和步骤线性规划问题就是求线性目标函数在线性约束条件下的最大值或最小值的问题.解决这类问题最常用、最重要的一种方法就是图解法.其步骤为:①画:画出可行域;②变:把目标函数变形为斜截式方程,从纵截距的角度寻找最优解;③求:解方程组求出最优解;④答:写出目标函数的最值.线性约束条件可行解最值线性约束设变量x,y满足约束条件x-y+2≥0,x-5y+10≤0,x+y-8≤0,则目标函数z=3x+4y的最大值为多少?【思路探究】线性规划问题【自主解答】画出约束条件表示的点(x,y)的可行域,如图所示的阴影部分(包括边界直线).把z=3x+4y变形为y=-34x+4z,得到斜率为-34,在y轴上的截距为4z,随z变化的一族平行直线.作直线l:y=-34x,把直线向右上方平行移至经过可行域上的点A,此时l1:y=-34x+4z的纵截距最大,同时z=3x+4y取最大值.解x-y+2=0,x+y-8=0得x=3,y=5,∴A(3,5).故当x=3,y=5时,zmax=29.变式1设变量x,y满足约束条件x-y+2≥0,x-5y+10≤0,x+y-8≤0,则目标函数z=4x+2y的最大值为多少?【自主解答】画出约束条件表示的点(x,y)的可行域,如图所示的阴影部分(包括边界直线).把z=4x+2y变形为y=-2x+2z,得到斜率为-2,在y轴上的截距为2z,随z变化的一族平行直线.作直线l:y=-2x,把直线向右上方平行移至经过可行域上的点B,此时l1:y=-2x+2z的纵截距最大,同时z=4x+2y取最大值.解x+y-8=0,x-5y+10=0得x=5,y=3,∴B(5,3).故当x=5,y=3时,zmax=26.变式2设变量x,y满足约束条件x-y+2≥0,x-5y+10≤0,x+y-8≤0,则目标函数z=3x-4y的最大值和最小值分别为多少.【解】作可行域如图所示,平移直线3x-4y=z可知,直线过A点时,z取最小值,过B点时,z取最大值.∴zmin=3×3-4×5=-11,zmax=3×5-4×3=3.1.由本例可以看出,解线性规划问题时,一定要注意最优解的对应点是最大值点,还是最小值点.对于目标函数z=ax+by(b≠0),当b>0时,直线截距最大时,z有最大值,截距最小时,z有最小值;当b<0时,则相反.2.图解法是解决线性规划问题的有效方法,其关键是利用z的几何意义求解.平移直线ax+by=0时,看它经过哪个点(哪些点)时最先接触可行域和最后离开可行域,则这样的点即为最优解,最优解一般是在可行域的边界取得.3.在平移目标函数时,一定要注意比较目标函数直线的斜率与可行域边界直线的斜率大小,防止直线的倾斜程度判断不准致误.利用线性规划求字母参数的值(或范围)已知x,y满足...