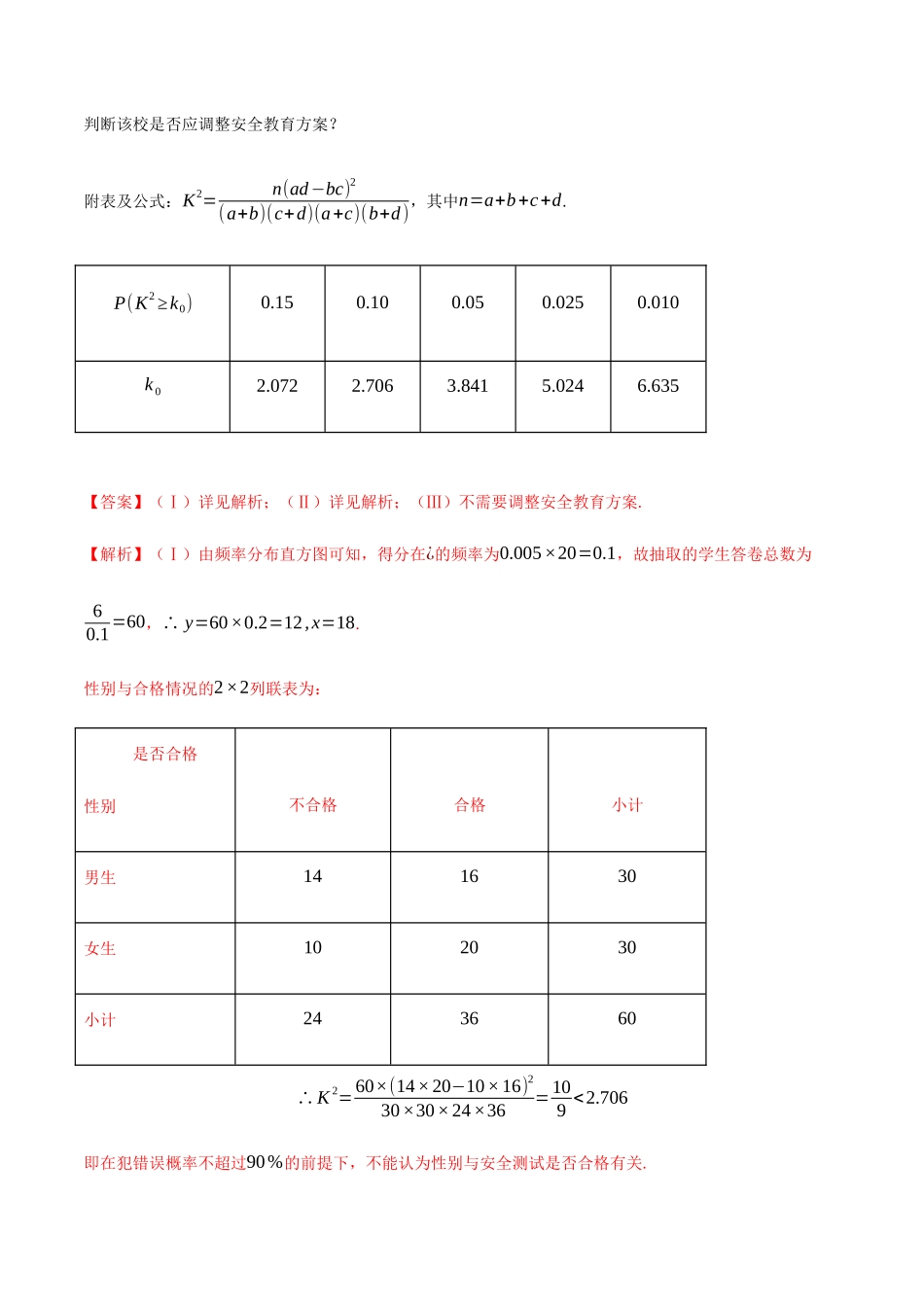
6.6独立性检验独立性检验:2×2列联表B合计An11n12n1+n21n22n2+总计n+1n+2n构造一个随机变量21122122121212nnnnnnnnn,利用随机变量χ2来判断“两个分类变量有关系”的方法称为独立性检验:若23.841,则有95%把握认为A与B有关;若26.635,则有99%把握认为A与B有关;其中23.841是判断是否有关系的临界值,23.841应判断为没有充分证据显示A与B有关,而不能作为小于95%的量化值来判断.【修炼套路】---为君聊赋《今日诗》,努力请从今日始【例1】某校为了解校园安全教育系列活动的成效,对全校学生进行一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的成绩,统计结果及对应的频率分布直方图如下所示:等级不合格合格【套路秘籍】---千里之行始于足下得分[20,40)[40,60)[60,80)[80,100)频数6x24y(Ⅰ)若测试的同学中,分数段¿、¿、¿、[80,100]内女生的人数分别为2人、8人、16人、4人,完成2×2列联表,并判断:是否有90%以上的把握认为性别与安全意识有关?是否合格性别不合格合格总计男生女生总计(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中,共选取10人进行座谈,现再从这10人中任选4人,记所选4人的量化总分为X,求X的分布列及数学期望E(X);(Ⅲ)某评估机构以指标M(M=E(X)D(X),其中D(X)表示X的方差)来评估该校安全教育活动的成效,若M≥0.7,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?附表及公式:K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d),其中n=a+b+c+d.P(K2≥k0)0.150.100.050.0250.010k02.0722.7063.8415.0246.635【答案】(Ⅰ)详见解析;(Ⅱ)详见解析;(Ⅲ)不需要调整安全教育方案.【解析】(Ⅰ)由频率分布直方图可知,得分在¿的频率为0.005×20=0.1,故抽取的学生答卷总数为60.1=60,∴y=60×0.2=12,x=18.性别与合格情况的2×2列联表为:是否合格性别不合格合格小计男生141630女生102030小计243660∴K2=60×(14×20−10×16)230×30×24×36=109<2.706即在犯错误概率不超过90%的前提下,不能认为性别与安全测试是否合格有关.(Ⅱ)“不合格”和“合格”的人数比例为24:36=2:3,因此抽取的10人中“不合格”有4人,“合格”有6人,所以X可能的取值为20、15、10、5、0,P(X=20)=C64C104=114,P(X=15)=C63C41C104=821,P(X=10)=C62C42C104=37,P(X=5)=C61C43C104=435,P(X=0)=C44C104=1210.X的分布列为:X20151050P114821374351210所以Eξ=20×114+15×821+10×37+5×435+0×1210=12.(Ⅲ)由(Ⅱ)知:D(X)=(20−12)2×114+(15−12)2×821+(10−12)2×37+(5−12)2×435+(0−12)2×1210=16∴M=E(X)D(X)=1216=34>0.7.故我们认为该校的安全教育活动是有效的,不需要调整安全教育方案.【举一反三】1.为推行“新课堂”教学法,某老师分别用传统教学和“新课堂”两种不同的教学方式在甲、乙两个平行班进行教学实验,为了解教学效果,期中考试后,分别从两个班级中各随机抽取20名学生的成绩进行统计,作出如图所示的茎叶图,若成绩大于70分为“成绩优良”.(1)由统计数据填写下面2×2列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”?甲班乙班总计成绩优良成绩不优良总计(2)从甲、乙两班40个样本中,成绩在60分以下(不含60分)的学生中任意选取2人,求抽取的2人中恰有一人来自乙班的概率.附:,()【答案】(1)见解析;(2)【解析】(1)根据茎叶图中的数据作出列联表如表所示:甲班乙班总计成绩优良101626成绩不优良10414总计202040根据列联表中的数据,得的观测值为,所以能在犯错误的概率不超过0.05的前提下认为“成绩优良与教学方式有关”.(2)样本中成绩在60分以下的学生中甲班有4人,乙班有2人,所以的所有可能取值为,,【运用套路】---纸上得来终觉浅,绝知此事要躬行1.我市某高中课题组通过随机询问名不同年级的学生是否能做到“扶跌倒老人”,得到如图所示的列联表,则下列结论正确的是()做不到能做到高...