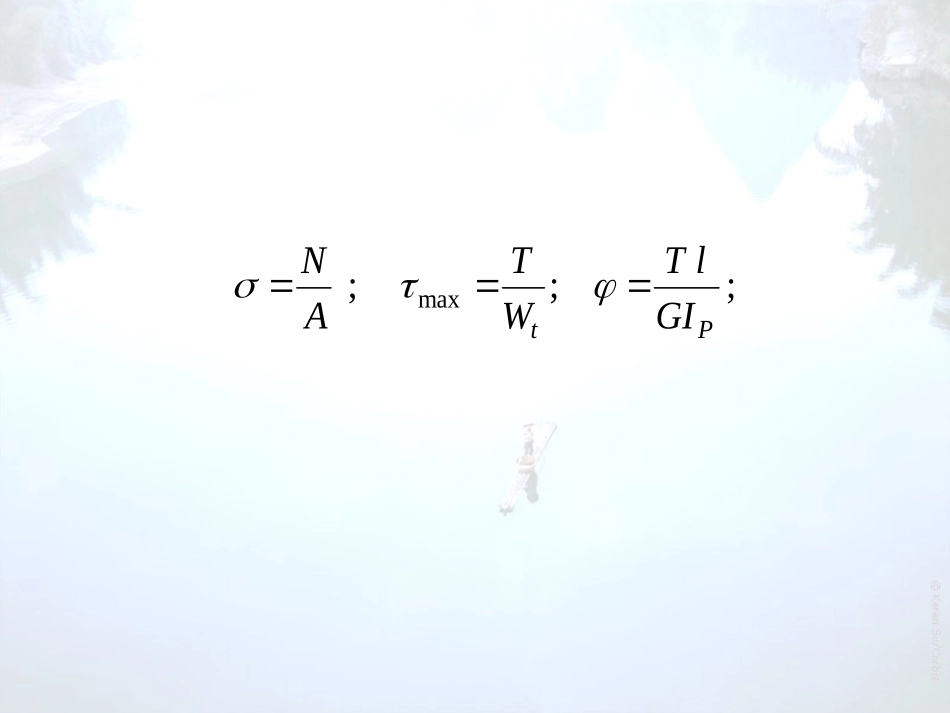材料力学(附录)VIP免费

;;;maxPtGIlTWTAN§I–1静矩和形心§I–2惯性矩和惯性半径§I–3惯性积§I–4平行移轴公式§I–5转轴公式主惯性轴附录I平面图形的几何性质一、静矩：AxAySddAxyyx定义：称为图形对x和y轴的静矩。（面积矩、一次矩）yxSS、AyAxSd§I-1静矩和形心二、形心：yASxAAxxAdASyASx则：xyxyCAAyyAdxASydAyxAxAySd（1）简单图形的形心和静矩：yASxASxy（2）组合图形的静矩和形心：ASxyASyxyxCyxyxCyxiAAydiiyAiiyiixxASyAS∴yx123AxAiiAyAii（3）图形有对称轴时，形心在对称轴上。（4）轴过形心。xSx00yASx0yCxydAxyyxyCxAAxxii109011010451090510110109011010510906510110解：组合图形，图形分割及坐标如图901201010xyC1C2[例I-2](P375)试确定下图的形心。AAyyii212121AAAxAx212121AAAyAy)mm(23)mm(38一、惯性矩：AxAyId2dAxyyx定义：Ix、Iy称为图形对x轴、y轴的惯性矩（量纲：[长度]4）AyAxId2§I-2惯性矩和惯性半径[例I-4]计算矩形对于其对称轴（形心轴）的惯性矩。yxChbdAydxdyAdAxAyId2解：Ayxydd222222dbbhhxdyy123bh123bhIx123hbIy计算圆形对于其对称轴（形心轴）的惯性矩。Cdxy[例I-5]ddAdddA解：AyxAyIId2sinyAxddI2)sin(ddd202203)(sinddd2020322cos1644dIxCdxydAxyAPAId2APAyxI)d(22AAPAydAxId22xyPIIIxPII2yxII极惯性矩：计算空心圆对于其对称轴（形心轴）的惯性矩。[例]DxyCdddIDdx202223)(sinddDd2022322cos1646444dDIx)1(6444DIx)(Dd三、惯性半径：AiIxx2AiIyy2ix和iy分别称为图形对于x轴和y轴的惯性半径。,AIixxAIiyy圆截面：AIixx4d46424dd四、组合图形的惯性矩：CxyixICxy1213AxAyId2iAAyd2iyyIIixxII§I–3惯性积dAxyyxAxyAxyIdIxy称为图形对x、y轴的惯性积。如果x轴（或y轴）是对称轴，则惯性积Ixy=0yyyxx-xAxyAxyIdyxChbCdxyIxy=0Ixy=0dACxCyCyCxC一、平行移轴公式：,,,ccccyxyxIII0CcxyASAxAyId2§I-4平行移轴公式已知：ayybxxCCxayb,xI求：AayACd)(2解：AaayyCACd)2(22AACACAaAyaAydd2d22AaaSIccxx22AaIIcxx2ba,,yIxyI注意:C点必须为形心AbIIcyy2abAIIcycxxyAaIIcxx2dAxyabCxCyCyCxC同理：[例]计算图示图形对其形心轴x轴和y轴的惯性矩。Cxy15104020单位：cm解：yx112AyAyii212211AAyAyA15402010201540452010cm)(25.26ixxII21xxII[例]计算图示图形对其形心轴x轴和y轴的惯性矩。Cxy15104020单位：cm解：yx112AyAyii212211AAyAyA15402010201540452010cm)(25.26ixxII21xxII12102031xI)cm(102.744a2)25.2645(1020Cxy15104020单位：cmyx11212401532xI)cm(103.104421xxxIII)cm(105.1710)3.102.7(444a2)2025.26(4015Cxy15104020单位：cmyx112iyyII21yyII12201031yI)cm(1067.044)cm(108.110)13.167.0(44421yyyIII12154032yI)cm(1013.1441216123xI)cm(10656.243[例]计算图示图形对其形心轴x轴的惯性矩。xCy28612单位：cm68解：1212103sincossincos11xyyyxx一、惯性矩和惯性积的转轴公式dAxyyxx1y1x1y1§I-5转轴公式主惯性轴,,,xyyxIII已知：1111,,yxyxIII求：解：AxAyId211AxAxyId)sincos(21αAAxyxyd)cossin2sincos(2222xAAAAxydAxdAydcossin2sincos2222AxAxyId)sincos(21AAxyxyd)cossin2sincos(2222cossin2sincos22xyyxIII...