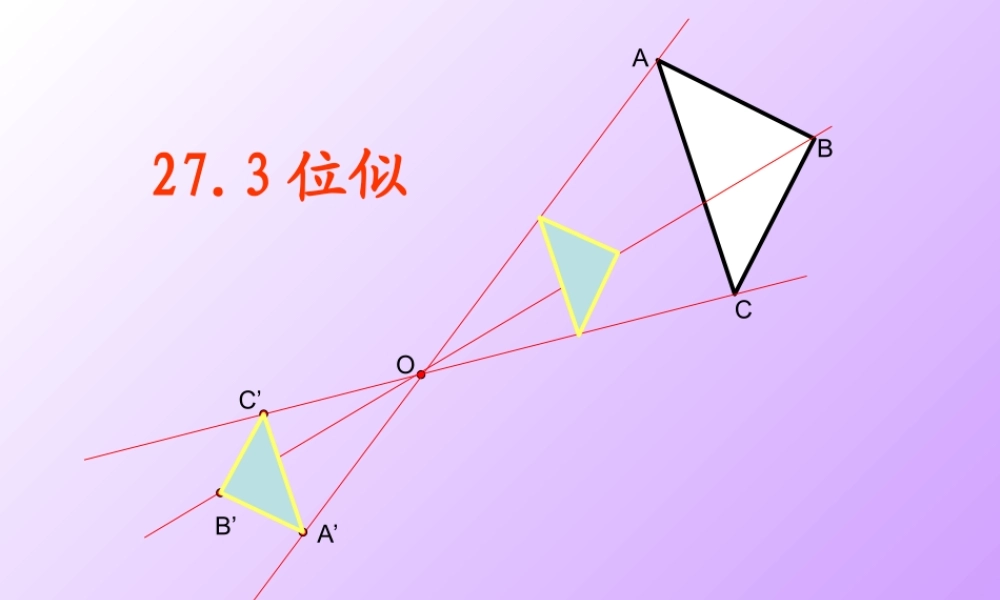
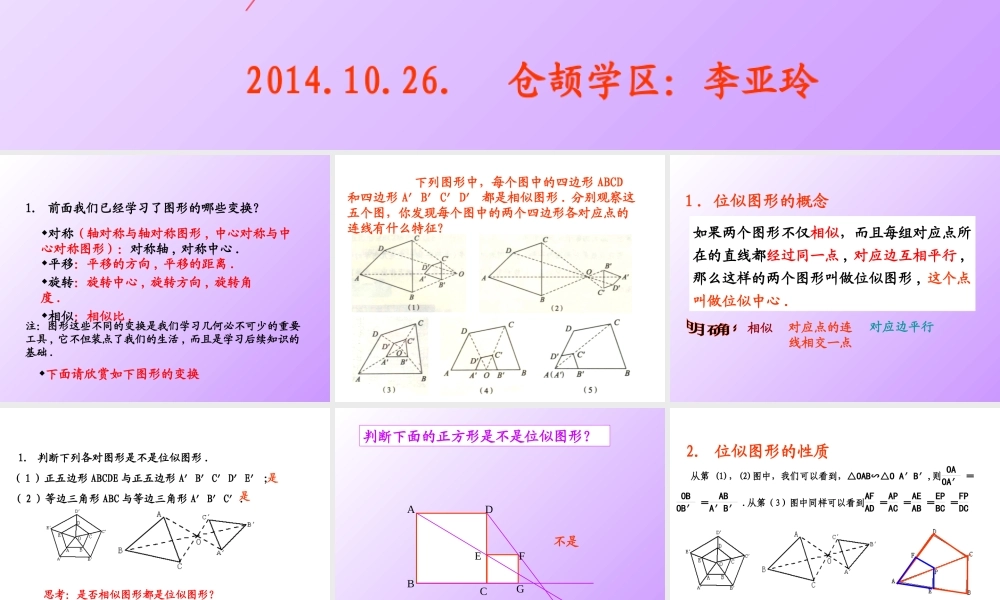
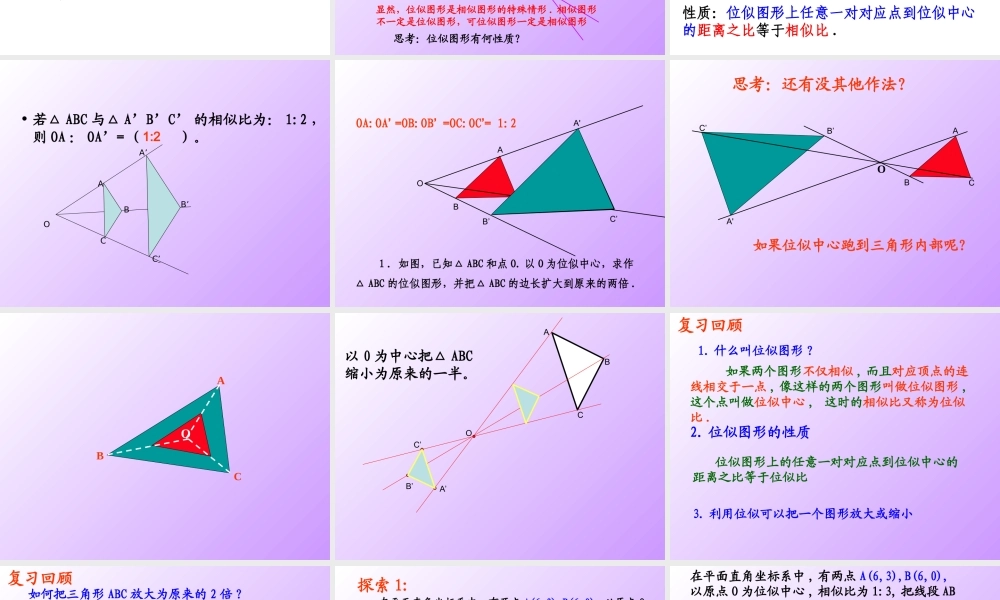
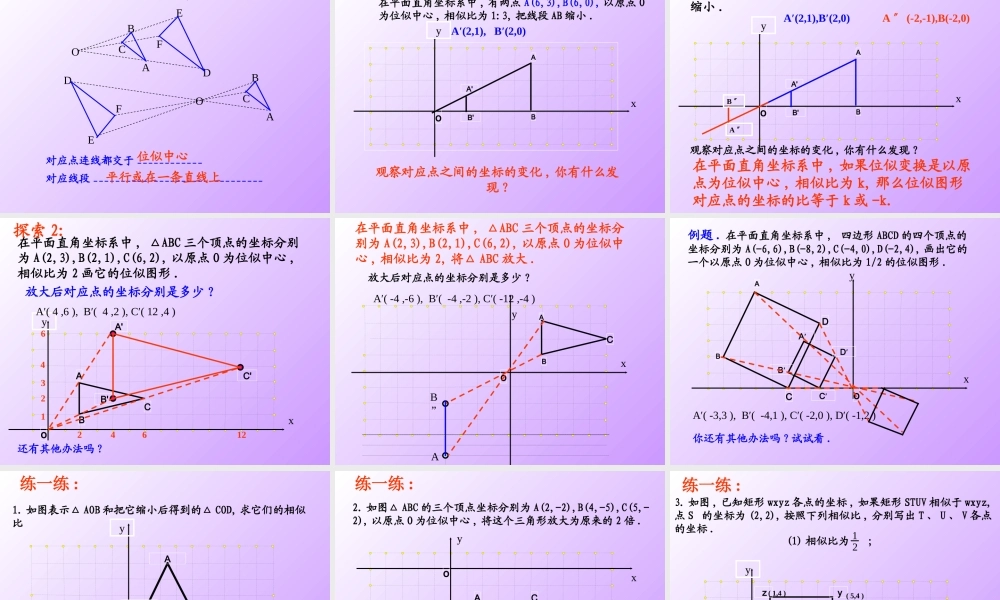
ABA’C’B’CO27.3 位似2014.10.26. 仓颉学区:李亚玲1. 前面我们已经学习了图形的哪些变换?平移:平移的方向 , 平移的距离 .旋转:旋转中心 , 旋转方向 , 旋转角度 .相似:相似比 .对称 ( 轴对称与轴对称图形 , 中心对称与中心对称图形 ) :对称轴 , 对称中心 .注:图形这些不同的变换是我们学习几何必不可少的重要工具 , 它不但装点了我们的生活 , 而且是学习后续知识的基础 .下面请欣赏如下图形的变换 下列图形中,每个图中的四边形 ABCD和四边形 A′B′C′D′ 都是相似图形 . 分别观察这五个图,你发现每个图中的两个四边形各对应点的连线有什么特征?1 .位似图形的概念如果两个图形不仅相似,而且每组对应点所在的直线都经过同一点 , 对应边互相平行 ,那么这样的两个图形叫做位似图形 , 这个点叫做位似中心 .相似对应点的连线相交一点对应边平行1. 判断下列各对图形是不是位似图形 . ( 1 )正五边形 ABCDE 与正五边形 A′B′C′D′E′ ; ( 2 )等边三角形 ABC 与等边三角形 A′B′C′.思考:是否相似图形都是位似图形?是是判断下面的正方形是不是位似图形?( 1)不是ACDBFEG显然,位似图形是相似图形的特殊情形 . 相似图形不一定是位似图形,可位似图形一定是相似图形 思考:位似图形有何性质?2. 位似图形的性质 从第 (1),(2)图中,我们可以看到,△OAB∽△O A′B′,则 OAOA′ =OBOB′ =ABA′B′ .从第(3)图中同样可以看到AFAD =APAC =AEAB =EPBC =FPDC 性质:位似图形上任意一对对应点到位似中心的距离之比等于相似比 . • 若△ ABC 与△ A’B’C’ 的相似比为: 1:2 ,则 OA : OA’= ( )。OAA’BCB’C’1:2O .ABCA'C’B’. 1 .如图,已知△ ABC 和点 O. 以 O 为位似中心,求作△ ABC 的位似图形,并把△ ABC 的边长扩大到原来的两倍 . OA:OA’ =OB:OB’ =OC:OC’= 1:2思考:还有没其他作法?O.ABA'C’B’C如果位似中心跑到三角形内部呢?ACBOABA’C’B’CO以 0 为中心把△ ABC缩小为原来的一半。 如果两个图形不仅相似 , 而且对应顶点的连线相交于一点 , 像这样的两个图形叫做位似图形 , 这个点叫做位似中心 , 这时的相似比又称为位似比 .1. 什么叫位似图形 ?2. 位似图形的性质 位似图形上的任意一对对应点到位似中心的距离之比等于位似比3. 利用位似可以把一个图形放大或缩小...