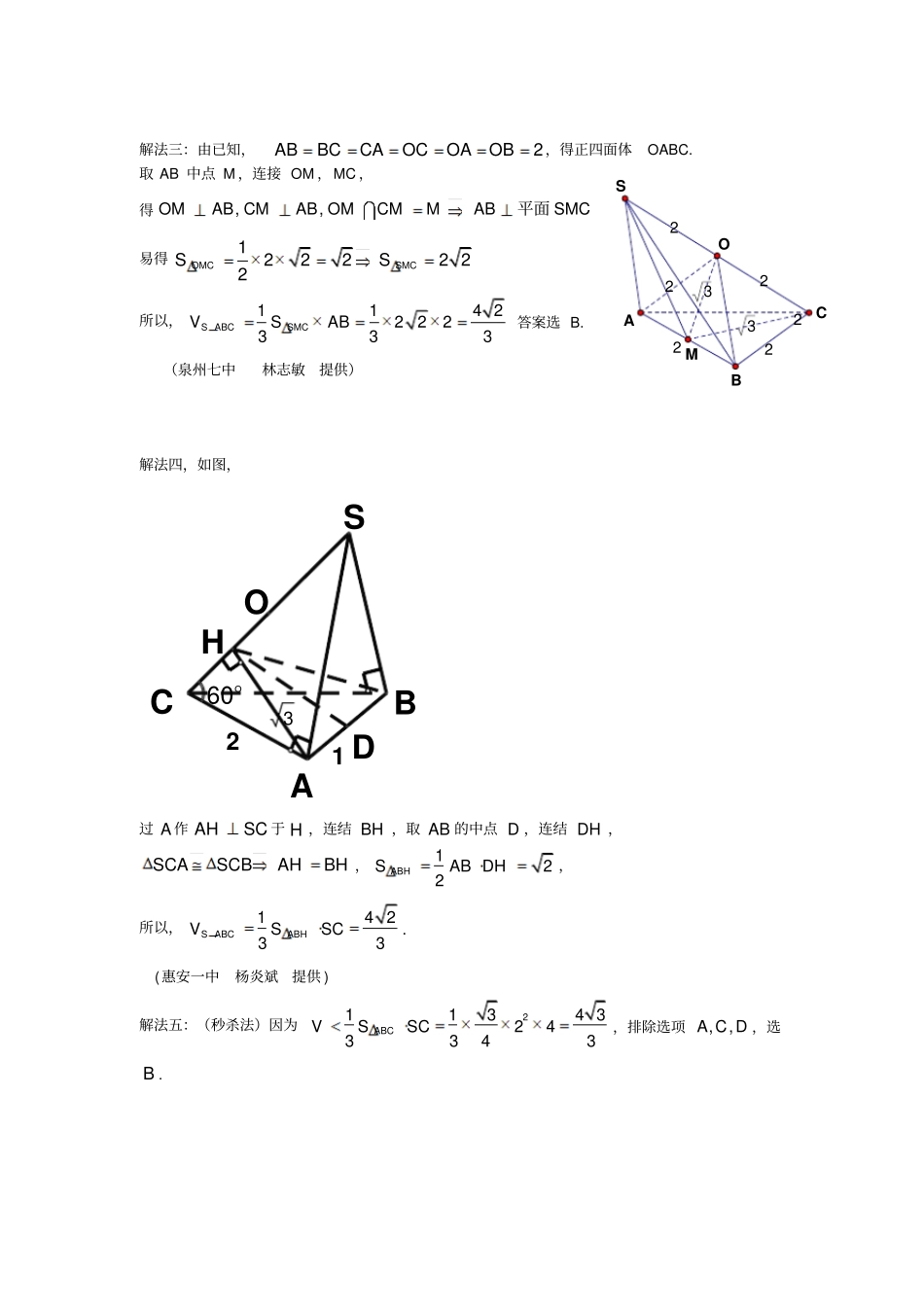
思维体操 .每日一题第 26 题( 2015、12、 2) (2012.新课标 . 理.11 改编)已知三棱锥 SABC 的所有顶点都在球O 的球面上 ,ABC 是边长为 2 的正三角形 , SC为球 O 的直径 , 且4SC, 则此棱锥的体积为( ) (A) 4 33(B) 4 23(C) 8 23(D) 4 2一.题目解法解法一:连接,OA OB ,易得棱锥 OABC 是边长为 2 的正四棱锥点 O在面 ABC 上的摄影是正ABC 的中心1O在1Rt OO C 中,1232 32323O C2OC,22112 63OOOCO C所以三棱锥的高14 623hOO21134 642233433ABCVSh选 B (莆田二中周顺华惠安高级中学张清强提供 ) 解法二:设1O 为ABC的中心,连接1O C 交球面于 H ,连接 SH ,则易证HCSH,又BCHB,SBBC所以 BC平面 SHB,SHBC,HCBCHSH平面 ABC又6ACH,可得364,334SHHC故3243644433131SHSVABC选 B (三明二中范训库提供)OO1BCHASOACBSO1解法三:由已知,2ABBCCAOCOAOB,得正四面体OABC. 取 AB 中点 M ,连接 OM ,MC ,得,,OMAB CMAB OMCMMABSMC平面易得12222 22OMCSMCSS所以,114 2222333S ABCSMCVSAB答案选 B. (泉州七中林志敏提供)解法四,如图,21360°DOCBSAH过 A 作 AHSC 于 H ,连结 BH ,取 AB 的中点 D ,连结 DH ,SCASCBAHBH ,122ABHSAB DH,所以,14 233S ABCABHVSSC.(惠安一中杨炎斌提供 ) 解法五:(秒杀法)因为21134 3243343ABCVSSC,排除选项,,A C D ,选B . 22222233MOACBS二.题目考点背景及高考链接与球有关的切、接问题福建省南安市第一中学高三备课组1.球的表面积公式:S= 4πR2;球的体积公式V=43πR32.与球有关的切、接问题中常见的组合:(1)正四面体与球:如图,设正四面体的棱长为a,内切球的半径为r,外接球的半径为R,取 AB 的中点为 D,连接 CD ,SE为正四面体的高,在截面三角形SDC 内作一个与边SD 和 DC 相切,圆心在高SE 上的圆.因为正四面体本身的对称性,内切球和外接球的球心同为O.此时, CO= OS=R,OE=r,SE=23a,CE=33 a,则有 R+r=23a,R2-r2= |CE|2=a23 ,解得 R=64 a,r=612 a.(2)正方体与球:①正方体的内切球:截面图为正方形EFHG 的内切圆,如图所示.设正方体的棱长为a,则 |OJ|=r=a2(r 为内切球半径 ).②与正方体各棱相切的球:截面图为正方形EFHG 的外接圆,则|GO|=R=22 a. ③正方体的外接球:截面图为正方形ACC1A1 的外接圆,则 |A1O|=R...