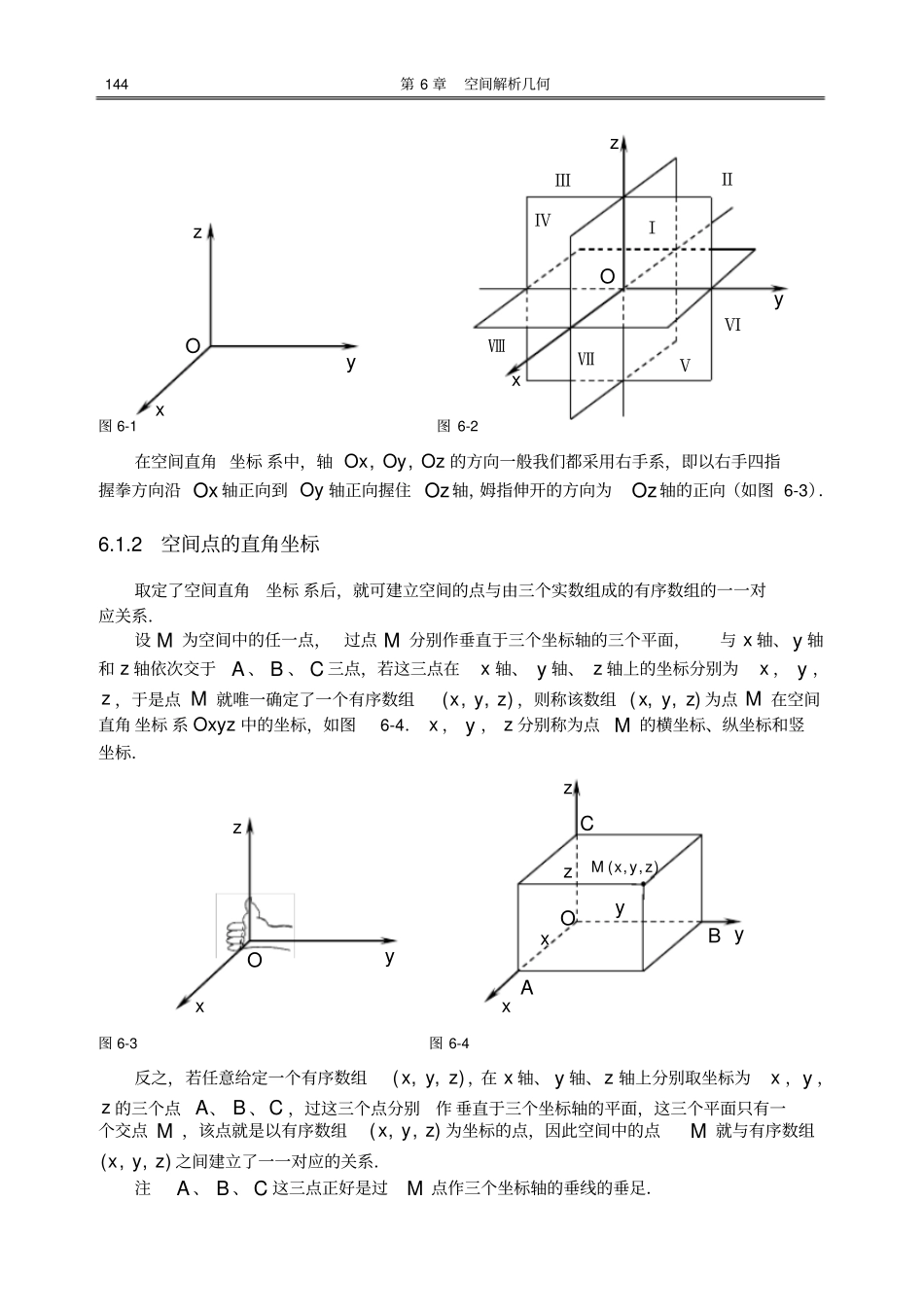
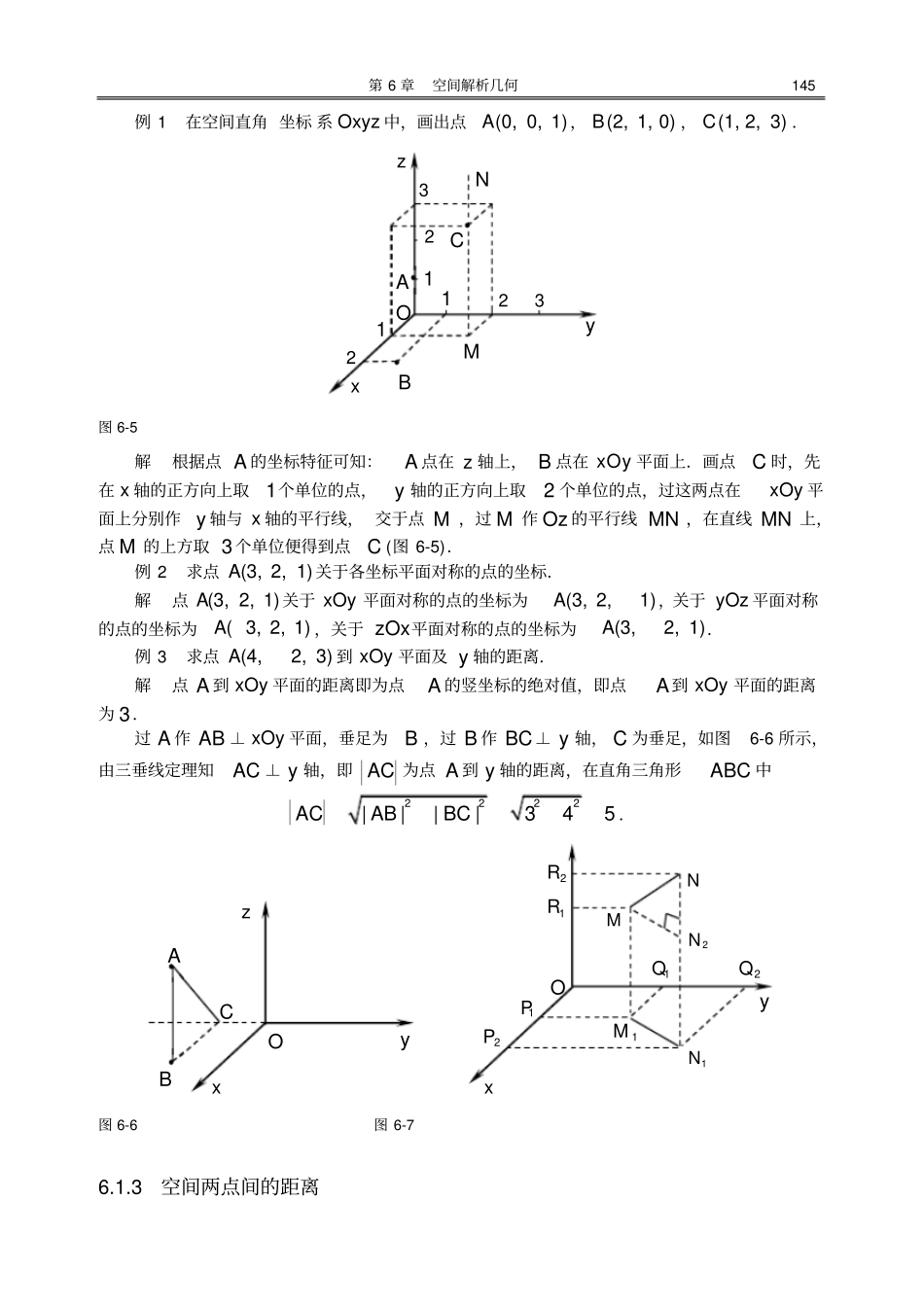
第 6 章空间解析几何空间解析几何是学习多元函数微积分的基础,空间向量是研究空间解析几何最有效的工具,它本身在工程技术中有着广泛的应用.本章将进一步研究空间向量,并以空间向量为工具讨论空间中的直线、平面、曲线与曲面.为了更方便地讨论以上问题,我们还要学习有关向量代数的基本知识.空间直角 坐标 系学时:2学时目的要求:1.理解空间直角坐标系是如何建立的以及如何确定空间点的坐标.2.能熟练运用空间两点间距离公式及中点坐标公式.为了确定直线上一点的位置,建立了数轴,用一个实数x 来确定该点 的位置;为了确定平面上一点的位置,建立了平面直角坐标系,用两个有序的实数组 ( ,)x y 来 确定该点 的位置;若想确定空间一点的位置,就需要建立新的坐标系,可以想到自然用三个有序实数来决定其位置.本节我们将通过空间直角坐标系,建立空间中的点与由三个实数组成的有序数组 的关系 ,即空间中点 与坐标之间的关系.6.1.1 空间直角 坐标系过空间一点 O ,作三条两两互相垂直的数轴,,Ox Oy Oz ,这样就构成了 空间直角坐标系,记作 Oxyz (如图 6-1).点 O 称为 坐标原点 ;三条轴,,Ox Oy Oz 统称为 坐标轴 ,分别简称为 横轴 、纵轴 和竖轴(竖轴也称为 立轴 );每两个坐标轴所决定的平面称为坐标平面 ,我们分别把它们叫做xOy平面, yOz 平面, zOx平面;这三个平面将空间划分成八个部分,称为空间直角坐标系的八个卦限 (如图 6-2).144 第 6 章空间解析几何图 6-1 图 6-2 在空间直角 坐标 系中,轴,,Ox Oy Oz 的方向一般我们都采用右手系,即以右手四指握拳方向沿 Ox 轴正向到 Oy 轴正向握住 Oz轴,姆指伸开的方向为Oz轴的正向(如图 6-3).6.1.2 空间点的直角坐标取定了空间直角坐标 系后,就可建立空间的点与由三个实数组成的有序数组的一一对应关系.设 M 为空间中的任一点, 过点 M 分别作垂直于三个坐标轴的三个平面,与 x 轴、 y 轴和 z 轴依次交于 A 、 B 、 C 三点,若这三点在x 轴、 y 轴、 z 轴上的坐标分别为x , y ,z ,于是点 M 就唯一确定了一个有序数组( ,,)x y z ,则称该数组 ( ,,)x y z 为点 M 在空间直角 坐标 系 Oxyz 中的坐标,如图6-4. x , y , z 分别称为点 M 的横坐标、纵坐标和竖坐标.图 6-3 图 6-4 反之,若任意给定一个有序数组( ,,)x y z ,在 x ...