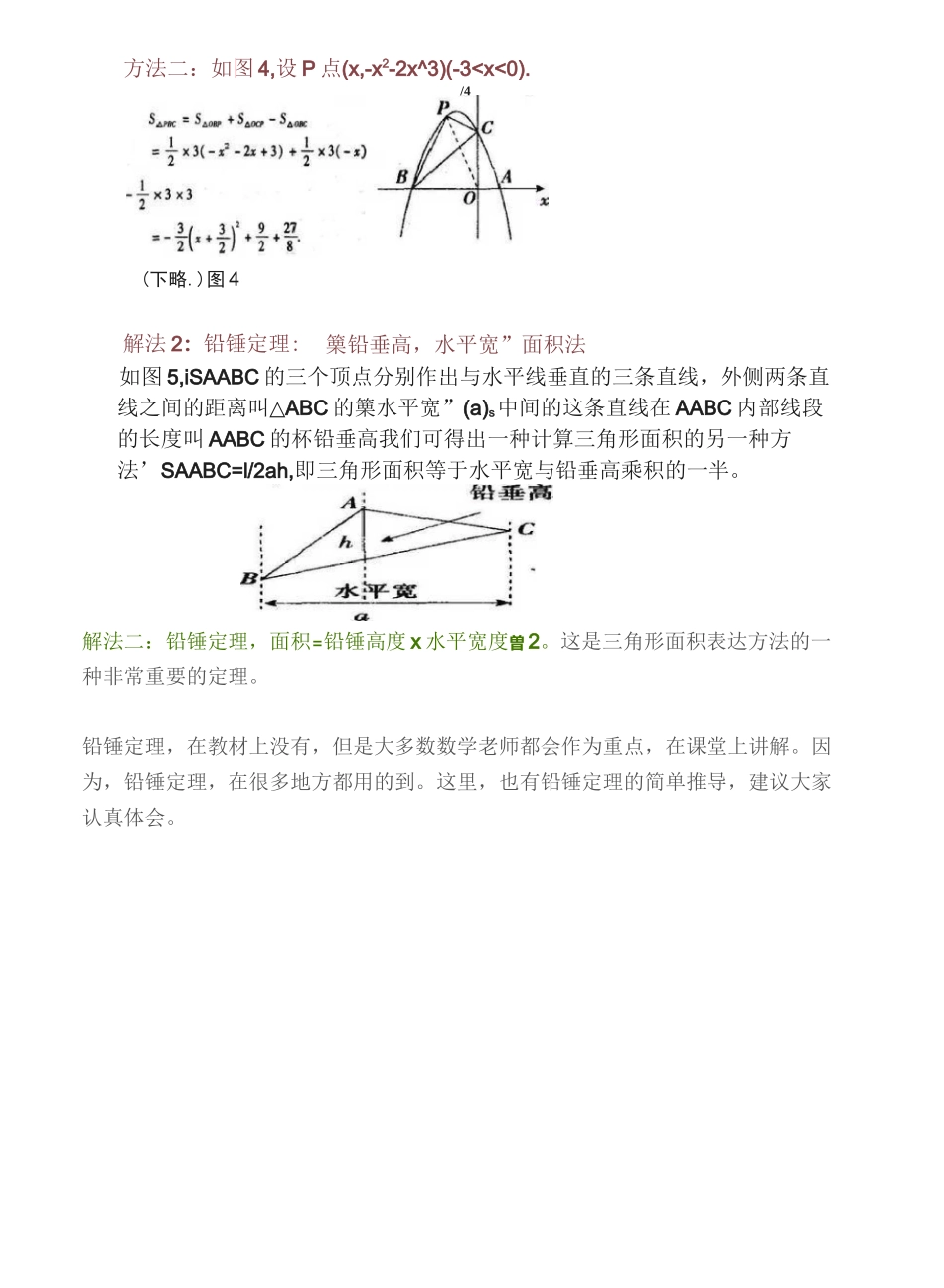
专题突破二次函数面积最值问题的 4 种解法,必看!二次函数是初中数学的一个重点,一个难点,也是中考数学必考的一个知识点。特别是在压轴题中,二次函数和几何综合出现的题型,才是最大的区分度。而求三角形面积的最值问题,更是常见。今天介绍二次函数考试题型中,面积最值问题的 4 种常用解法。同学们,只要熟练运用一两种解法,炉火纯青,在考试答题的时候,能够轻松答题,就好。从近几年的各地中考试卷来看,求面积的最值问题在压轴题中比较常见,而且通常与二次函数相结合◎在这里以一道中考题为例,介绍几种不同的解题方法,供同学们参考,都掌握了之后一定会在压轴题上有一个大的提升-例题:如图 1■,抛物线 y=-x2+bx+c 与 x 轴交于 A⑴0),BL3,0)两点。⑴ 求该抛物线的解析式;⑵ 设⑴中的抛物线交 Y 轴于 C 点,在该抛物线的对称轴上是否存在点 Q 使得 AQAC 的周长最小?若存在,求出 Q 点的坐标;若不存在,请说明理由,⑶ 如图 2,在⑴中的抛物线上的第二象限上是否存在一点 P,使 APBC 的面积最大?若存在,求出点 P 的坐标及△PBC 的面积最大值;若没有,请说明理由「一tJ・q■■■=■IliITT■-d原题:在(1)中的抛物线上的第二象限是否存在一点 P,使 APBC 的面积最大?若存在,求出 P 点的坐标及 APBC 的面积最大值,若没有,请说明理由。考试题型,大多类似于此。求面积最大值的动点坐标,并求出面积最大值。一般解题思路和步骤是,设动点 P 的坐标,然后用代数式表达各线段的长。通过公式计算,得出二次函数顶点式,则坐标和最值,即出。解帛⑴ 抛物线解析式为尸-*-力站(2)将军饮马问题,求出 Q(-b2);下面着重探讨求第(3)小题中面积最大值的几种方法.解法 1:补形'割形法几何图形中常见的处理方式有分割、补形等,此类方法的要点在于把所求图形的面积进行适当的补或割,变成有利于表示面积的图形。方法:如图 3,设 P 点(X,-x2-2x+3)(-3