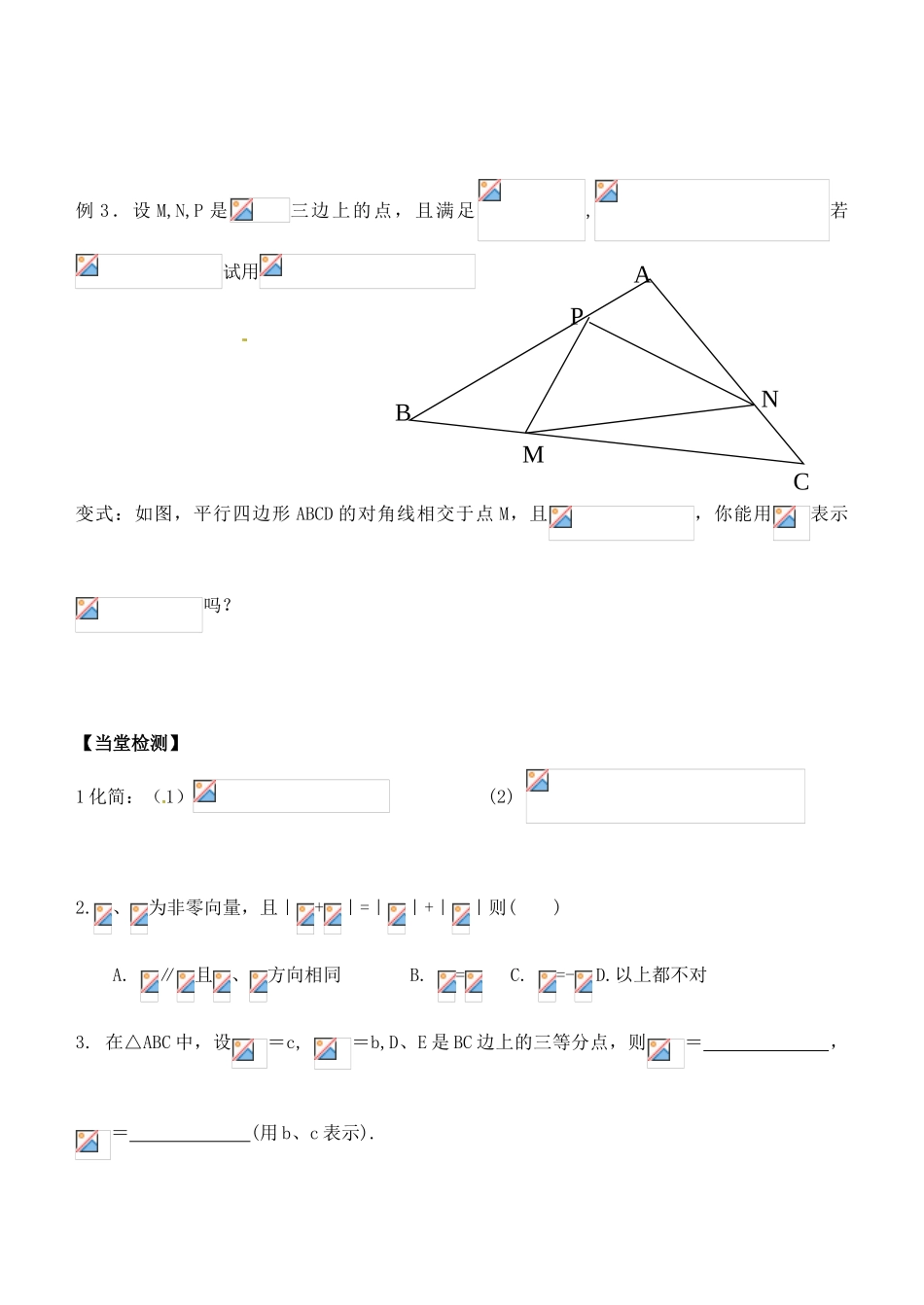
山东省郯城第三中学高一数学《向量数积的几何意义》学案【学习目标】1. 掌握实数与向量积的定义,理解实数与向量数积的几何意义;2. 让学生能由实数运算律类比向量数乘运算律,并且验证强化对知识的形成过程的认识,正确表示结果,掌握实数与向量的积的运算律;3. 能熟练运用实数与向量积的定义,运算律进行有关计算.【重点、难点】实数向量积的几何意义,用运算律进行计算。自主学习案【知识梳理】1. 向量的数乘我们规定实数与向量的积是一个向量,这种运算叫作向量的数乘,记作 .它的长度和方向规定如下:(1)|λ|= ;(2)λ>0 时 λ与方向 ;λ<0 时 λ与方向 ;由(3)知 λ=0 或=时,λ= ,方向 ;2. 实数与向量积的几何意义当|λ|>1 时,表示向量的有向线段在原方向(>0)或反方向(<0)上伸长到原来的 倍,当 0<|λ|<1 时,表示向量的有向线段在原方向(>0)或反方向(<0)上到缩短到原来的____ 倍. 3.实数与向量积的运算律(1) 结合律:λ(μ)= ;(2)分配律:(λ+μ)= ,λ(+)=______ ;4.如果()与共线,那么有且只有一个实数,使 5.若存在使得 ,则三点 A,B,C 共线.【预习 自测】1、 设则下列叙述不正确的是( )A. B. C. D. 的方向与向量的方向相同2. 已知若且向量的方向与向量的方向相反,则 λ 的值为( )A . 2 B.-2 C. D. 3. 设是任意的两个向量,,给出下面四个结论:(1)若与共线,则 (2)若,则与共线;(3)若,则与共线,(4)若则有使得其中,正确的结论有 ( )A.(1)(2) B. (1)(3) C. (1)(3)(4) D. (2)(3)(4)【我的疑问】合作探究案【课内探究】例1.化简(1) (2) 例 2. 如图,已知任意两个非零向量试作你能判断 A,B,C 三点之间的关系吗?为什么?变式:设两个非零向量和不共线,如果=2+3,=6+23, =4-8,求证:A、B、D 三点共线.例 3.设 M,N,P 是三边上的点,且满足,若试用 变式:如图,平行四边形 ABCD 的对角线相交于点 M,且,你能用表示吗?【当堂检测】1 化简:(1) (2) 2.、为非零向量,且|+|=||+||则( )A. ∥且、方向相同B. = C. =-D.以上都不对3. 在△ABC 中,设=c, =b,D、E 是 BC 边上的三等分点,则= ,= (用 b、c 表示).ABCPMN课后练习案1. 设则下列叙述正确的是( )A. B. C. D. 与向量是共线向量. 2.化简_______________.3.已知=,=λ,则 λ 的值为( )A.- B.- C. D.4. 已知梯形 ABCD 中,且=2,M、N 分别为 CD、AB 的中点,若=a,=b,用a、b 表示.5. 已知任意两个非零向量,设,求证:A,B,D 三点共线。6. △ABC 中, =,EF∥BC 交 AC 于 F 点,设=,=,试用,表示向量。