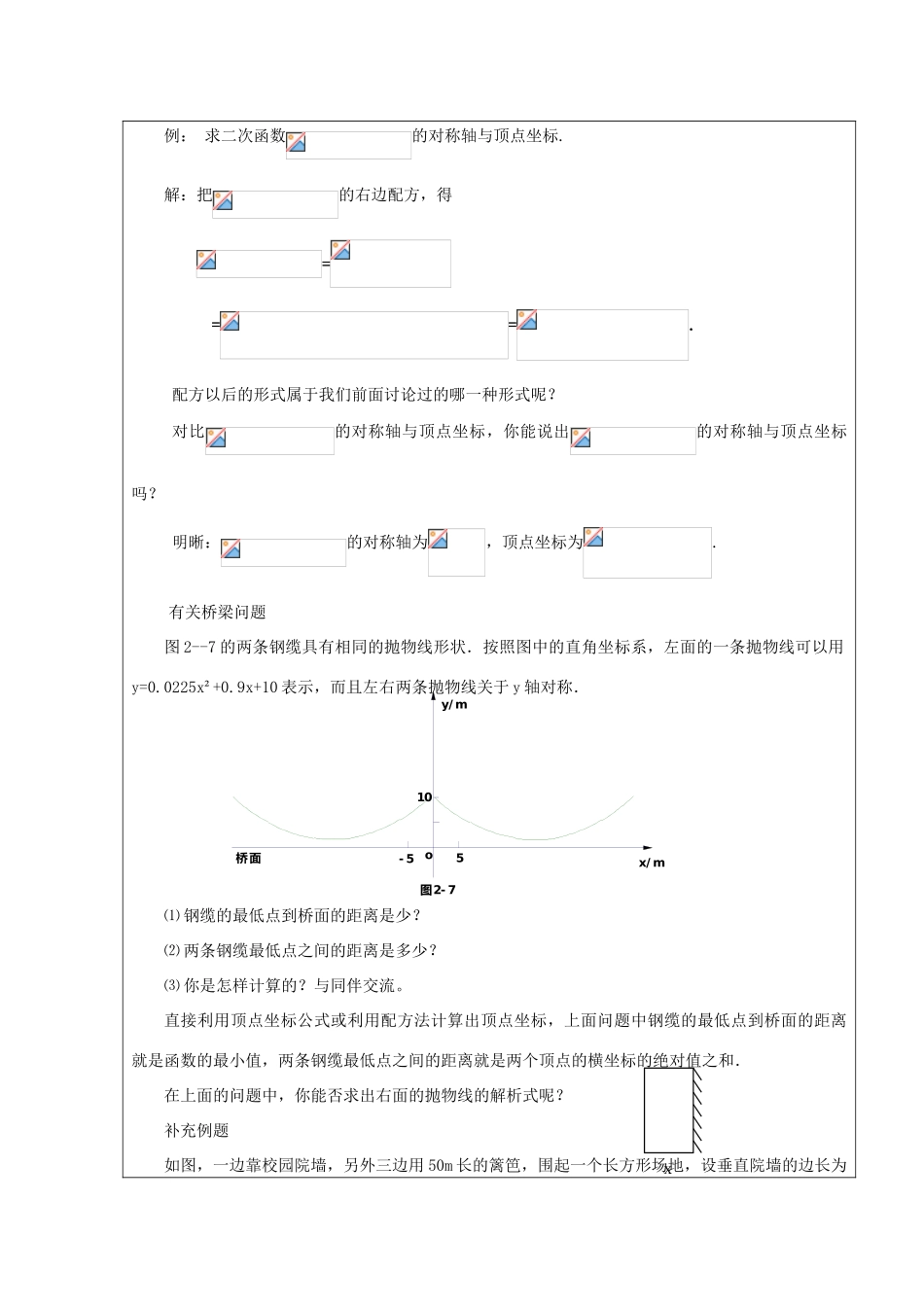
教学内容2.4二次函数的图象(二)设计者沈晓丽第1课时/总2课时设计日期教学目标知识与能力1.体会建立二次函数对称轴和顶点坐标公式的必要性.2.能够运用二次函数的对称轴和顶点坐标公式解决问题.过程与方法1.通过解决实际问题,培养学生把数学知识运用于实践的能力.2.通过学生合作交流来解决问题,培养学生合作交流的能力.情感价值观1.经历将一些实际问题抽象为数学问题的过程,掌握数学的基础知识和基本技能,并能解决简单的问题.2.差别认识数学与人类生活的密切联系及对人类历史发展的作用.教学重点运用二次函数的对称轴和顶点坐标公式解决问题教学难点把数学问题与实际问题相联系的过程.教学方法讲解法教学活动过程设计一.创设问题情景,引入新课上节课我们主要讨论了函数,的图象的有关性质,特别练习了求函数的对称轴与顶点坐标.学习的目的是为了应用,那么究竟有什么用呢?今天我们来学习二次函数的应用.二.讲解新课例题:指出函数,,,的对称轴与顶点坐标.对于二次函数(),它属于上面形式的哪一种呢?还是另一种呢?它的对称轴与顶点坐标是什么?例:求二次函数的对称轴与顶点坐标.解:把的右边配方,得===.配方以后的形式属于我们前面讨论过的哪一种形式呢?对比的对称轴与顶点坐标,你能说出的对称轴与顶点坐标吗?明晰:的对称轴为,顶点坐标为.有关桥梁问题图2--7的两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x²+0.9x+10表示,而且左右两条抛物线关于y轴对称.⑴钢缆的最低点到桥面的距离是少?⑵两条钢缆最低点之间的距离是多少?⑶你是怎样计算的?与同伴交流。直接利用顶点坐标公式或利用配方法计算出顶点坐标,上面问题中钢缆的最低点到桥面的距离就是函数的最小值,两条钢缆最低点之间的距离就是两个顶点的横坐标的绝对值之和.在上面的问题中,你能否求出右面的抛物线的解析式呢?补充例题如图,一边靠校园院墙,另外三边用50m长的篱笆,围起一个长方形场地,设垂直院墙的边长为ࣜ�图2-7ࣜ�桥面ࣜ�oࣜ�x/mࣜ�y/mࣜ�10ࣜ�5ࣜ�-5xxm.(1)写出长方形场地面积y(m2)与x的函数关系式;(2)画出函数的图象;(3)求边长为多少时,长方形面积最大,最大是多少?三、课堂练习随堂练习1.根据公式确定下列二次函数图象的对称轴和顶点坐标:(1)(2);(3);(4)四小结谈谈学了本节课你有什么收获?板书设计二次函数的图象(二)例题(投影)有关桥梁问题(投影)补充例题课堂练习作业布置教学反思备注:教案可有改动痕迹,教学反思手写完成。