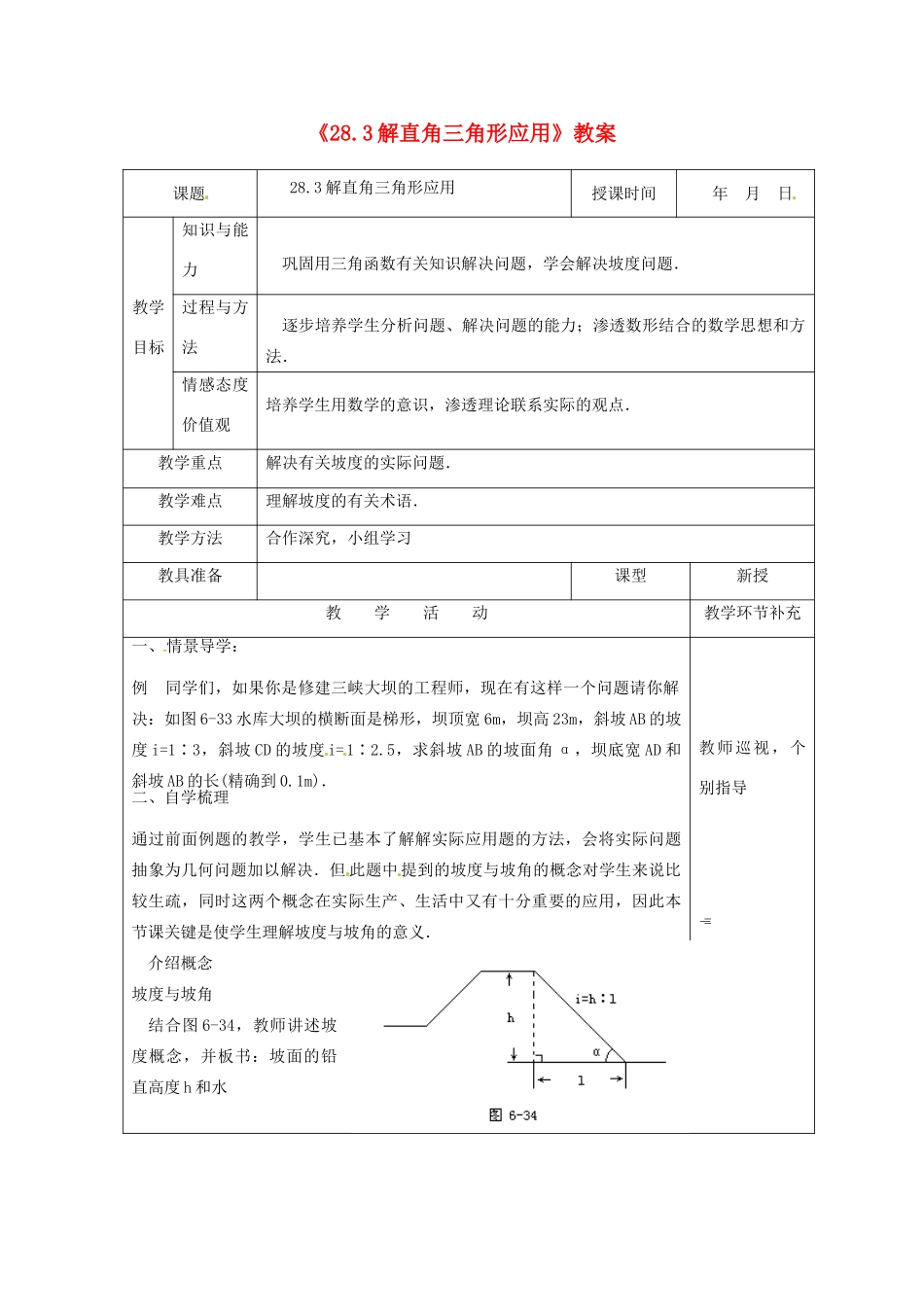
《28.3解直角三角形应用》教案课题28.3解直角三角形应用授课时间年月日教学目标知识与能力巩固用三角函数有关知识解决问题,学会解决坡度问题.过程与方法逐步培养学生分析问题、解决问题的能力;渗透数形结合的数学思想和方法.情感态度价值观培养学生用数学的意识,渗透理论联系实际的观点.教学重点解决有关坡度的实际问题.教学难点理解坡度的有关术语.教学方法合作深究,小组学习教具准备课型新授教学活动教学环节补充一、情景导学:例同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图6-33水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m).二、自学梳理通过前面例题的教学,学生已基本了解解实际应用题的方法,会将实际问题抽象为几何问题加以解决.但此题中提到的坡度与坡角的概念对学生来说比较生疏,同时这两个概念在实际生产、生活中又有十分重要的应用,因此本节课关键是使学生理解坡度与坡角的意义.介绍概念坡度与坡角结合图6-34,教师讲述坡度概念,并板书:坡面的铅直高度h和水教师巡视,个别指导平宽度的比叫做坡度(或叫做坡比),一般用i表示。即i=,把坡面与水平面的夹角α叫做坡角.引导学生结合图形思考,坡度i与坡角α之间具有什么关系?答:i==tan三、合作解疑:这一关系在实际问题中经常用到,教师不妨设置练习,加以巩固.练习(1)一段坡面的坡角为60°,则坡度i=______;______,坡角______度.为了加深对坡度与坡角的理解,培养学生空间想象力,教师还可以提问:(1)坡面铅直高度一定,其坡角、坡度和坡面水平宽度有什么关系?举例说明.(2)坡面水平宽度一定,铅直高度与坡度有何关系,举例说明.答:(1)如图,铅直高度AB一定,水平宽度BC增加,α将变小,坡度减小,因为tan=,AB不变,tan随BC增大而减小(2)与(1)相反,水平宽度BC不变,α将随铅直高度增大而增大,tanα也随之增大,因为tan=不变时,tan随AB的增大而增大四、点拨校正(师生共同分析,总结归纳)引导学生分析例题,图中ABCD是梯形,若BE⊥AD,CF⊥AD,梯形就被分割成Rt△ABE,矩形BEFC和Rt△CFD,AD=AE+EF+FD,AE、DF可在△ABE和△CDF中通过坡度求出,EF=BC=6m,从而求出AD.以上分析最好在学生充分思考后由学生完成,以培养学生逻辑思维能力及良好的学习习惯.坡度问题计算过程很繁琐,因此教师一定要做好示范,并严格要求学生,选择最简练、准确的方法计算,以培养学生运算能力.五、巩固应用:教材P124.2六、课堂小结:说说你在本节课的收获。七、达标检测:(见学案)板书设计:28.3解直角三角形应用