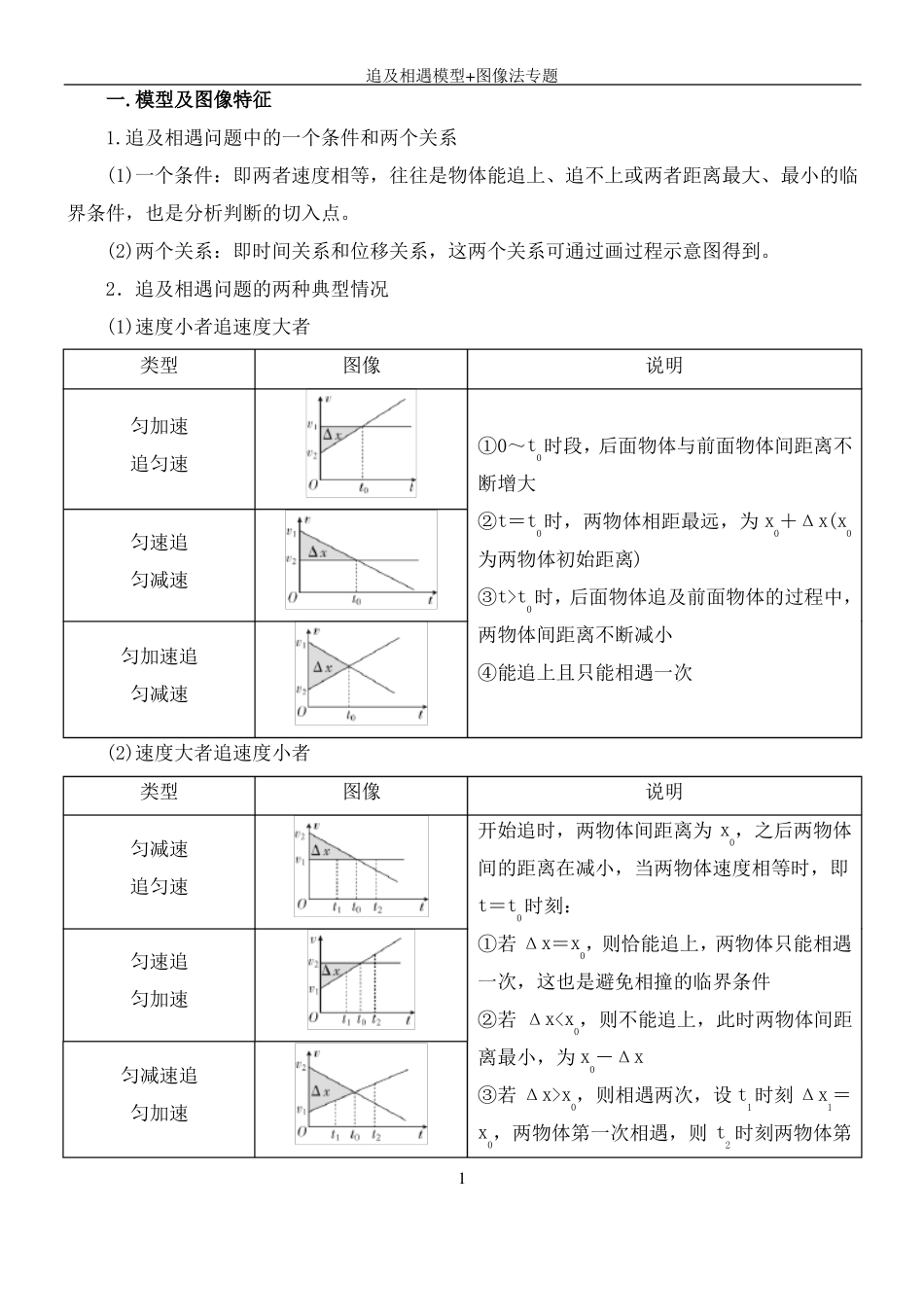
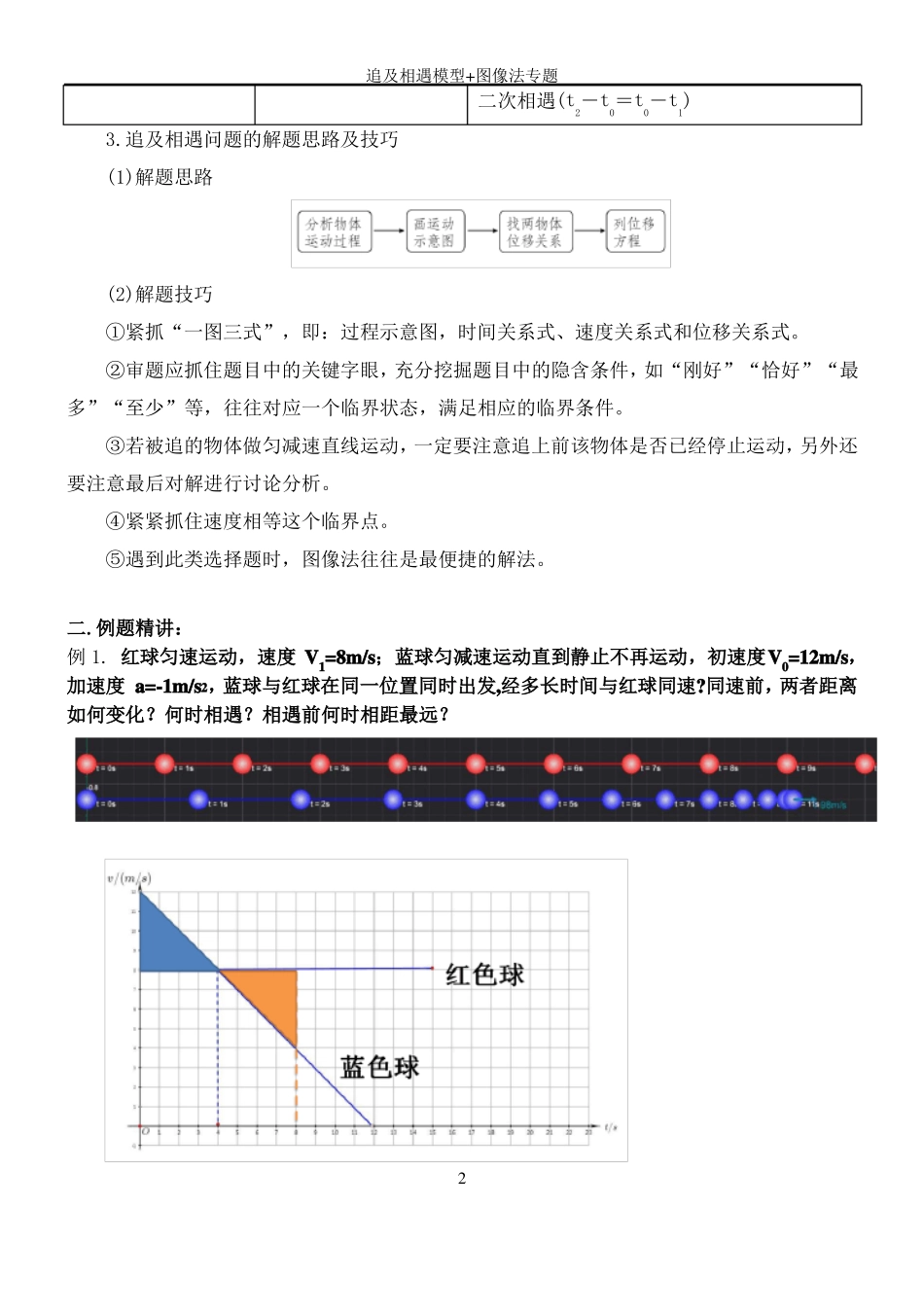
追及相遇模型+图像法专题一.模型及图像特征1.追及相遇问题中的一个条件和两个关系(1)一个条件:即两者速度相等,往往是物体能追上、追不上或两者距离最大、最小的临界条件,也是分析判断的切入点。(2)两个关系:即时间关系和位移关系,这两个关系可通过画过程示意图得到。2.追及相遇问题的两种典型情况(1)速度小者追速度大者类型匀加速追匀速匀速追匀减速匀加速追匀减速图像说明①0~t0时段,后面物体与前面物体间距离不断增大②t=t0时,两物体相距最远,为x0+Δx(x0为两物体初始距离)③t>t0时,后面物体追及前面物体的过程中,两物体间距离不断减小④能追上且只能相遇一次(2)速度大者追速度小者类型匀减速追匀速匀速追匀加速匀减速追匀加速图像说明开始追时,两物体间距离为x0,之后两物体间的距离在减小,当两物体速度相等时,即t=t0时刻:①若Δx=x0,则恰能追上,两物体只能相遇一次,这也是避免相撞的临界条件②若Δxx0,则相遇两次,设t1时刻Δx1=1x0,两物体第一次相遇,则t2时刻两物体第追及相遇模型+图像法专题二次相遇(t2-t0=t0-t1)3.追及相遇问题的解题思路及技巧(1)解题思路(2)解题技巧①紧抓“一图三式”,即:过程示意图,时间关系式、速度关系式和位移关系式。②审题应抓住题目中的关键字眼,充分挖掘题目中的隐含条件,如“刚好”“恰好”“最多”“至少”等,往往对应一个临界状态,满足相应的临界条件。③若被追的物体做匀减速直线运动,一定要注意追上前该物体是否已经停止运动,另外还要注意最后对解进行讨论分析。④紧紧抓住速度相等这个临界点。⑤遇到此类选择题时,图像法往往是最便捷的解法。二.例题精讲:例1.红球匀速运动,速度V1=8m/s;蓝球匀减速运动直到静止不再运动,初速度V0=12m/s,加速度a=-1m/s2,蓝球与红球在同一位置同时出发,经多长时间与红球同速?同速前,两者距离如何变化?何时相遇?相遇前何时相距最远?2追及相遇模型+图像法专题答案:4s,增大,8s,4s变式1:红球匀速运动,初速度V1=8m/s;蓝球匀减速运动直到静止不再运动,初速度V0=12m/s,加速度a=-1m/s,蓝球在红球后8m,经多长时间与红球同速?何时相遇?还能再次相遇吗?2答案:4s,4s第一次相遇,不能再次相遇。变式2:红球匀速运动,速度V1=8m/s;蓝球匀减速运动直到静止不再运动,初速度V0=12m/s,加速度a=-1m/s,蓝球在红球后10m,经多长时间与红球同速?能相遇吗?何时最近?2答案:4s,不能相遇,4s变式3:红球匀速运动,速度V1=8m/s;蓝球匀减速运动直到静止不再运动,初速度V0=12m/s,加速度a=-1m/s,蓝球在红球后6m,两球何时同速?何时相遇?两球距离是怎样变化的?23追及相遇模型+图像法专题答案:4s,2s和6s,两次相遇之间,距离先增大后减小,同速时相距最远变式4:红球匀速运动,速度V1=4m/s;蓝球匀减速运动直到静止不再运动,初速度V0=12m/s,加速度a=-1m/s,蓝球在红球后14m,两球何时同速?何时相遇?2答案:8s,2s和14.5s变式5:红球匀速运动,速度V1=4m/s;蓝球匀减速运动直到静止后立即反向加速,初速度V0=12m/s,加速度大小始终为1m/s。蓝球在红球后14m,两球何时同速?何时相遇?42追及相遇模型+图像法专题答案:8s,2s和14s注意事项:减速运动分为不可返回和可返回减速运动,对于不可返回运动,要先计算减速到0所需的时间。例2一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以a=3m/s的加速度开始行驶,恰在这一时刻一辆自行车以v自=6m/s的速度匀速驶来,从旁边超过汽车。试求:(1)汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?(2)什么时候汽车能追上自行车?此时汽车的速度是多少?答案:(1)2_s__6_m__(2)4_s__12_m/s(1)解法一(物理分析法):如图甲所示,汽车与自行车的速度相等时相距最远,设此时经过的时间为t1,汽车和自行车间的距离为Δx,则有v自=at1所以t1=2v自=2sa12Δx=v自t1-at1=6m。2解法二(相对运动法):以自行车为参考系,则从开始到相距最远的这段时间内,汽车相对这个参考系的各个物理量为初速度v0=v汽初-v自=0-6m/s=-6m/s末速度vt=v...