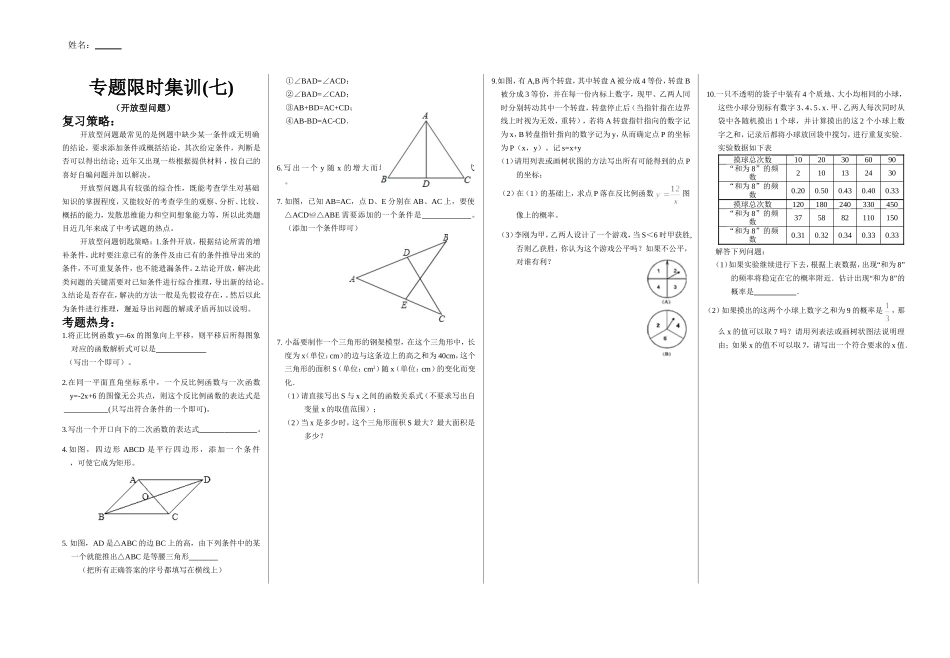
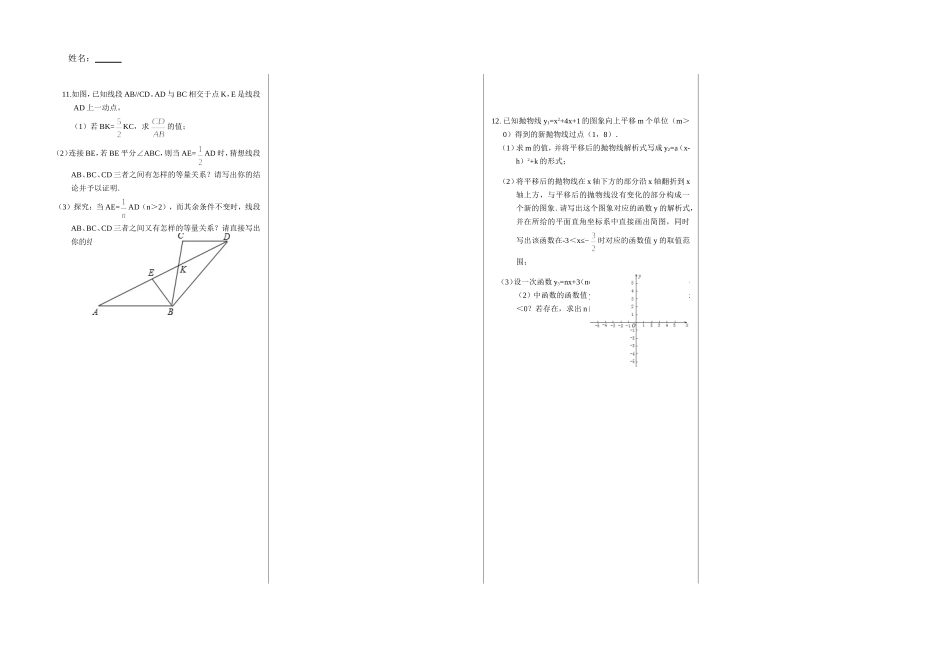
专题限时集训(七)(开放型问题)复习策略:开放型问题最常见的是例题中缺少某一条件或无明确的结论,要求添加条件或概括结论,其次给定条件,判断是否可以得出结论;近年又出现一些根据提供材料,按自己的喜好自编问题并加以解决。开放型问题具有较强的综合性,既能考查学生对基础知识的掌握程度,又能较好的考查学生的观察、分析、比较、概括的能力,发散思维能力和空间想象能力等,所以此类题目近几年来成了中考试题的热点。开放型问题钥匙策略:1.条件开放,根据结论所需的增补条件,此时要注意已有的条件及由已有的条件推导出来的条件,不可重复条件,也不能遗漏条件。2.结论开放,解决此类问题的关键需要对已知条件进行综合推理,导出新的结论。3.结论是否存在,解决的方法一般是先假设存在,。然后以此为条件进行推理,邂逅导出问题的解或矛盾再加以说明。考题热身:1.将正比例函数y=-6x的图象向上平移,则平移后所得图象对应的函数解析式可以是(写出一个即可)。2.在同一平面直角坐标系中,一个反比例函数与一次函数y=-2x+6的图像无公共点,则这个反比例函数的表达式是(只写出符合条件的一个即可)。3.写出一个开口向下的二次函数的表达式。4.如图,四边形ABCD是平行四边形,添加一个条件,可使它成为矩形。5.如图,AD是△ABC的边BC上的高,由下列条件中的某一个就能推出△ABC是等腰三角形(把所有正确答案的序号都填写在横线上)①∠BAD=ACD∠;②∠BAD=CAD∠;③AB+BD=AC+CD;④AB-BD=AC-CD.6.写出一个y随x的增大而增大的一次函数的解析式。7.如图,已知AB=AC,点D、E分别在AB、AC上,要使△ACDABE≌△需要添加的一个条件是。(添加一个条件即可)7.小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);(2)当x是多少时,这个三角形面积S最大?最大面积是多少?9.如图,有A,B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字,现甲、乙两人同时分别转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y)。记s=x+y(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;(2)在(1)的基础上,求点P落在反比例函数图像上的概率。(3)李刚为甲,乙两人设计了一个游戏,当S<6时甲获胜,否则乙获胜,你认为这个游戏公平吗?如果不公平,对谁有利?10.一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3、4、5、x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表摸球总次数1020306090“和为8”的频数210132430“和为8”的频数0.200.500.430.400.33摸球总次数120180240330450“和为8”的频数375882110150“和为8”的频数0.310.320.340.330.33解答下列问题:(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是.(2)如果摸出的这两个小球上数字之和为9的概率是,那么x的值可以取7吗?请用列表法或画树状图法说明理由;如果x的值不可以取7,请写出一个符合要求的x值.姓名:11.如图,已知线段AB//CD。AD与BC相交于点K,E是线段AD上一动点。(1)若BK=KC,求的值;(2)连接BE,若BE平分∠ABC,则当AE=AD时,猜想线段AB、BC、CD三者之间有怎样的等量关系?请写出你的结论并予以证明.(3)探究:当AE=AD(n>2),而其余条件不变时,线段AB、BC、CD三者之间又有怎样的等量关系?请直接写出你的结论,不必证明.12.已知抛物线y1=x2+4x+1的图象向上平移m个单位(m>0)得到的新抛物线过点(1,8).(1)求m的值,并将平移后的抛物线解析式写成y2=a(x-h)2+k的形式;(2)将平移后的抛物线在x轴下方的部分沿x轴翻折到x轴上方,与平移后的抛物线没有变化的部分构成一个新...