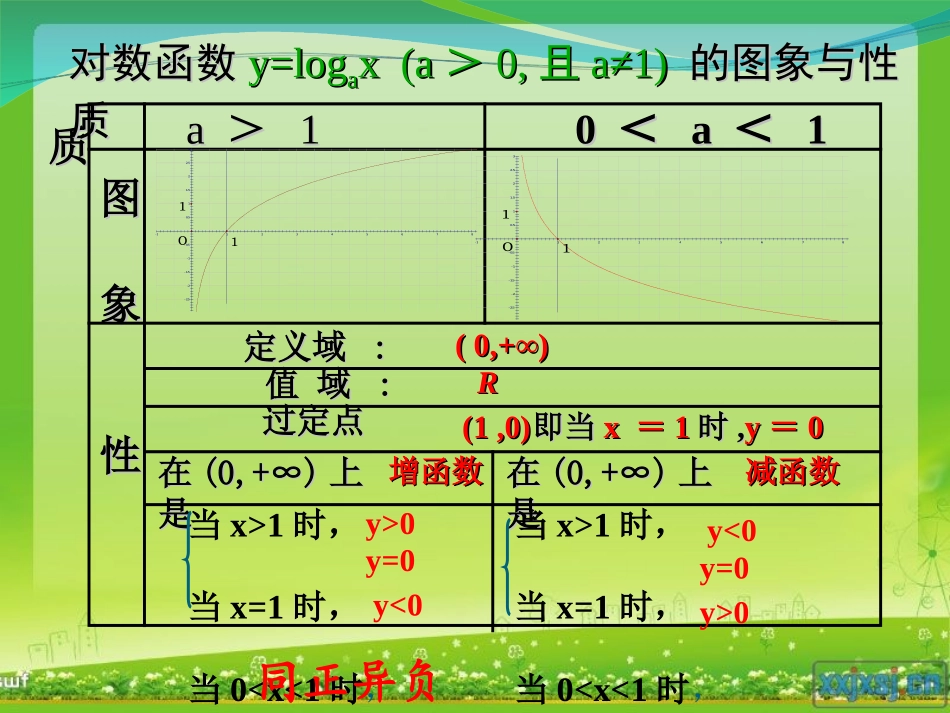
对数函数及其应用图图象性象性质质aa>>1100<<aa<<11定义域定义域::值域值域::过定点过定点在在(0,+∞)(0,+∞)上上是是在在(0,+∞)(0,+∞)上上是是对数函数对数函数y=logy=logaax(ax(a>>0,0,且且a≠1)a≠1)的图象与性的图象与性质质当x>1时,当x=1时,当00y=0y<0当x>1时,当x=1时,当0032.521.510.5-0.5-1-1.5-2-2.5-11234567801132.521.510.5-0.5-1-1.5-2-2.5-112345678011同正异负回顾指数函数及其性质的应用:题型1:过定点问题题型2:利用单调性比较大小题型3:利用单调性解不等式题型4:求指数型复合函数的单调区间题型5:求指数型复合函数的值域题型一:对数型函数的过定点问题例1:.log(32)5(01)ayxaa函数且的图象恒过定点性质:对数函数恒过定点(1,0).log(01)ayxaa,且1,5.3y解:令3x+2=1,则x=-1,5).3所以函数的图象恒过定点(-练习:函数的图像恒过定点.2log(5)3,(0,1)ayxxaa且方法总结:令对数型函数的真数部分等于1.(3,3),(2,3).例1.求下列函数的定义域:xy2log1)1(xy311log)2(7xy3log)3(1log)4(5.0xy解:00log2xx01loglog22xx01xx∴函数的定义域是),1()1,0(解:0311x031x31x∴函数的定义域是)31,(解:00log3xx01loglog33xx01xx∴函数的定义域是),1[解:001log5.0xx05.0log1log5.05.0xx05.0xx∴函数的定义域是]5.0,0(二、关于比较两个函数值的大小1.先找出对应的函数模型(1)若为两个同底的对数值看做同底的对数函数(2)若为两个同底的指数幂看做同底的指数函数(3)若为两个同指数的指数幂看做同指数的幂函数2.再确定对应的函数的增减性3.最后由单调性的定义比较大小4.注意学会化数为函数的技能,如:)10(,10aaa且,1log0a,log1aa3ln)1(5ln3.0log)2(e3.0log23.1)3(例2.比较下列各值的大小33.12.03.0)4(5.03.01.0)5(1.014.33.02)6(3.03,0ln)是增函数,+在(对数函数xy,0log3.0)是减函数,+在(对数函数xy,3.1上是增函数在指数函数Ryx,3.0上是减函数在指数函数Ryx,01.0)是减函数,+在(幂函数xy,03.0)是增函数,+在(幂函数xy2log)7(3.002.0log)8(3.011log03.03.0log13.0<><<<<>>三、关于解指数或对数不等式例3.解下列不等式)1(222)1(xx)1(log)32(log)2(3.03.0xx上是增函数在Ryx2)1(222)1(2xxxx由2x解得上是减函数在),0(log3.0xy03201132xxxx223x解得小结:1.解指数(或对数)不等式,就是利用函数的单调性去掉指数(或对数)符号转化为普通不等式求解;2.去掉指数(或对数)符号时要注意不等号的方向,即当为增函数时,去掉函数符号后不等号不变;当是减函数时,去掉函数符号后不等号反向;3.解对数不等式时,还要同时解真数部分大于0。题型三:利用对数函数的单调性解不等式例4:(1)已知,求x的范围.0.70.7log(2)log(1)xx1(2)log1,2aa已知求的取值范围.0.7()log0+fxx解:(1)函数在(,)上为减函数.由已知得:201021xxxx解得x>1.+不等式的解集为(1,).11(2)log1loglog,22aaaa由得11,,2aa若有此时无解.1101,,1.22aaa若有所以1,12a综上,的取值范围为().注意:对数的真数必须大于0.化同底log(31)1,aaa练习:已知求的取值范围.log(31)1log(31)log,aaaaaa解:由得11,,310aaaa3若有此时无解.31101,,,01.3103aaaaaa若有得所以0,1a综上,的取值范围为().题型四:对数型复合函数的单调性2log(2)yx0.3log(32)yx例5:(1)分析函数的单调性.(2)分析函数的单调性解:(1)x-2>0,即x>2,函数的定义域为(2,+).2()2,log,(0,)tgxxytt令则2()(2,)logtgxyt在上为增...