复数的综合应用VIP免费

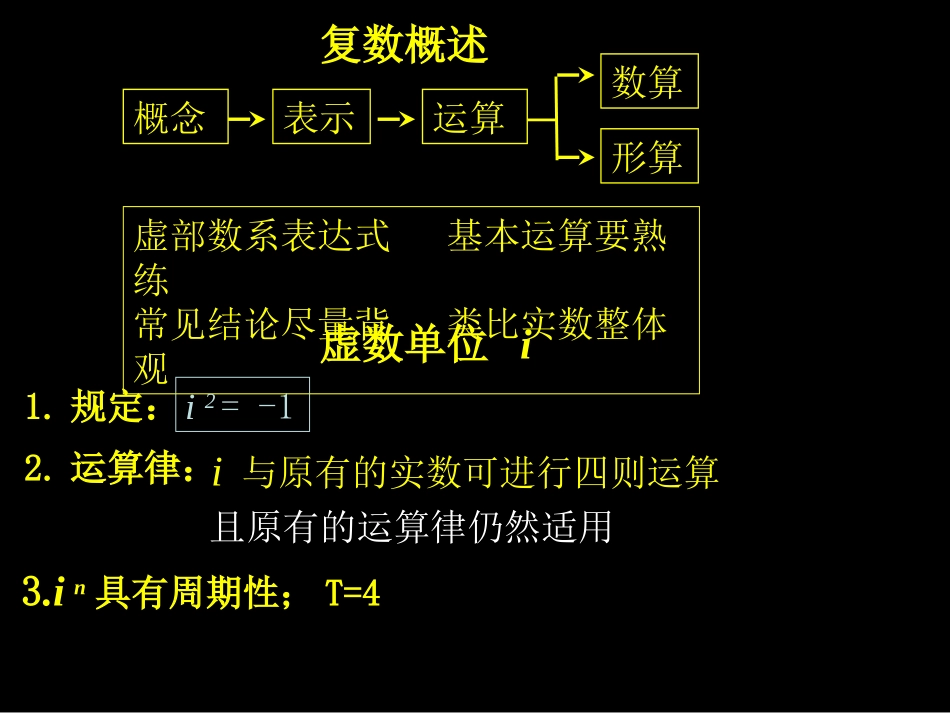
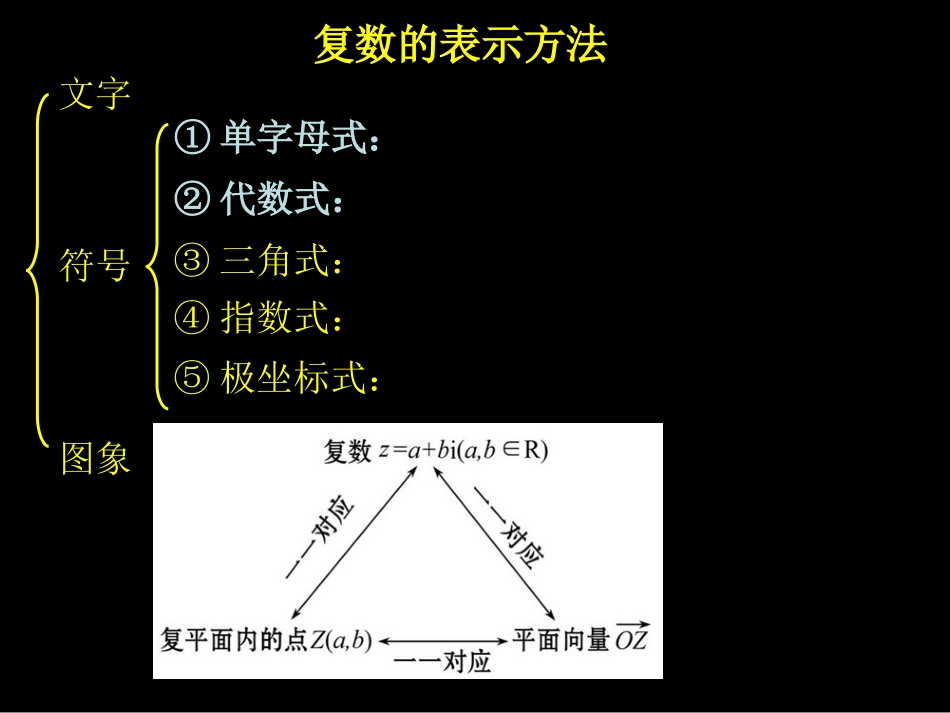
一、虚部数系要清楚灵活选用表达式二、混合运算是重点模仿实数整体观三、代数基本大定理常见结论要了解§235复数的综合应用复数概述概念表示运算数算形算虚部数系表达式基本运算要熟练常见结论尽量背类比实数整体观1.规定：虚数单位ii2=-12.运算律：i与原有的实数可进行四则运算且原有的运算律仍然适用iiiiiinnnn3424144,1,,13.in具有周期性；T=4复数的表示方法文字符号图象④指数式：①单字母式：②代数式：③三角式：⑤极坐标式：,,,,,;,,,2121zzzzzzyixbia;)sin(cosirrire数系复数实数虚数非纯虚数纯虚数虚数集复数集实数集纯虚数集(a+bi)(b＝0)(a=0且b≠0)(b≠0)(ab≠0)数系复数实数虚数非纯虚数纯虚数虚数集复数集实数集纯虚数集yox复数实数纯虚数数系复数实数虚数非纯虚数纯虚数虚数集复数集实数集纯虚数集yox非纯虚数复数相等共轭复数复数的模22||baz注：复平面中即点Z1与点Z2重合注：复平面中即点Z与点Z关于实轴对称注：复平面中即向量的模OZ||21zz即向量的模21ZZ加减法运算idbcadicbia①交换律：z1+z2=z2+z11.法则：2.运算律：注：类似于多项式的加减法运算②结合律：(z1+z2)+z3=z1+(z2+z3)乘法运算ibcadbdacdicbia)()(2.运算律：1.法则：注：类似于多项式的乘法运算①交换律：z1·z2=z2·z1②结合律：(z1·z2)·z3=z1·(z2·z3)③分配律：z1(z2+z3)=z1·z2+z1·z3除法运算注：类似于分母有理化，分母实数化，化除法为乘法,但满足二项式定理乘方运算nnnzzzz2121)(4.一般的，nnnzzzz2121)(3.mnnmzz)(2.nmnmzzz1.5.特殊的有②平方和(差)公式：③完全平方和(差)公式：①in具有周期性；T=4))((22biabiabaiiiiiinnnn3424144,1,,1abibabia2)(222ii2)1(2()模的运算||||||||||212121zzzzzz||||||2121zzzz||||||2121zzzznnzz||||2.公式：③1.定义：22||baz注：复平面中即向量的模OZ①②④||21zz即向量的模21ZZazz2_共轭运算⑤①②③④zz⑦bizz2_2_||zzz2121zzzz2121zzzz2121)(zzzz⑥复数与复平面内的点及向量是1—1对应的biaz:复数yoxba上图仅仅说明了：OZ②并非说：复数就是向量遗传：加减法的几何意义相同①复数z=a+bi与复平面中的是1—1对应的关系变异：乘法不相同；复数有除法，向量无除法……复数四则运算的几何意义1.复数加减法的几何意义：模乘模，角加角(三角式)可按照向量加减法的几何意义来进行(代数式)2.复数乘法的几何意义：模除模，角减角(三角式)3.复数除法的几何意义：2121OZOZzz是纯虚数对应的向量互相平行、是实数2121zzzz特例①：特例②：一、虚部数系要清楚灵活选用表达式二、混合运算是重点模仿实数整体观三、代数基本大定理常见结论要了解§235复数的综合应用(1)(2013年新课标Ⅰ变式)若复数z满足则z的虚部为______②4i⑧⑤④－4i①4③－4⑥⑦5454i54i54⑤一、虚部数系要清楚灵活选用表达式(2)(2013年上海)设m∈R,是纯虚数【-2】则m=_______二、混合运算是重点模仿实数整体观(3)(2012年福建)若复数z满足zi＝1－i，则z=A．－1－iB．1－iC．－1＋iD．1＋i【A】法1：设z=x+yi……法2：zi=1-i–两端乘i……z2zz2)(izz，则z=(4)(2014年江西)是z的共轭复数.若且zA.1+iB.1-iC.-1+iD.-1-i【B】法1：设z=x+yi……法2：由得z-=-2i2)(izz……将其与相加可得2zz法1：设z=x+yi……()(2)5zii,则z=(5)(2012年安徽)复数z满足：A.-2-2iB.-2+2iC.2-2iD.2+2i【D】法2：两端乘2+i得z-i=2+i……()(2)5zii(7)若复数z满足：z(2-3i)=6+4i，则|z|=_______【2】法1：设z=x+yi……法2：z(2-3i)=6+4i两端同时取模可得……512izi(6)(2013年重庆)已知复数，则|z|=_______法1：将z改写成x+yi……的形式法2：两端同时取模可得……512izi5三、代数基本大定理常见结论要了解1.一元n次方程有n个根,伟大定理仍然成立2.实系数一元n次方程的虚根是共轭成对出现的3.虚系数一元n次方程至少有一个虚根i2102cbxxA.b...