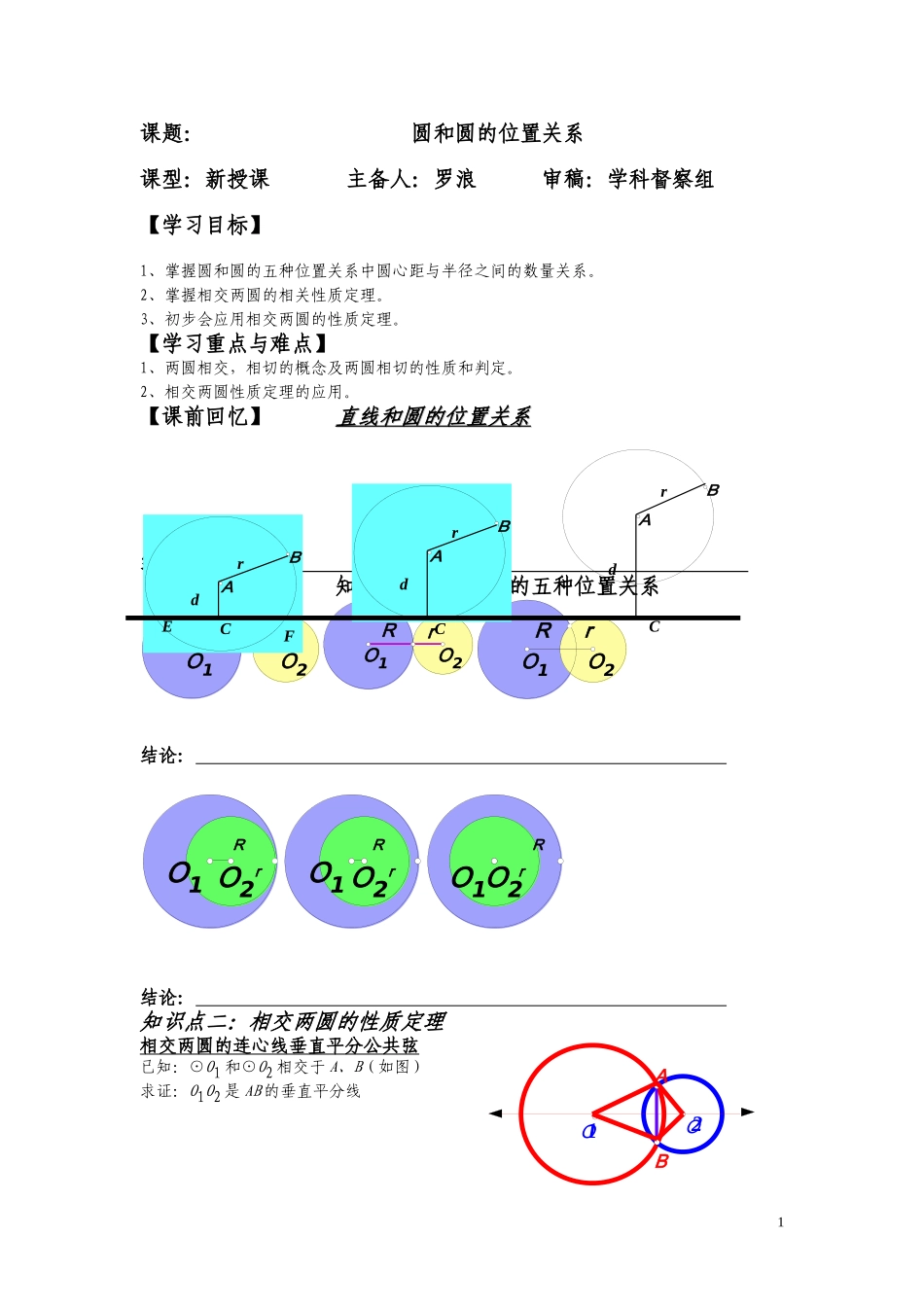
课题:圆和圆的位置关系课型:新授课主备人:罗浪审稿:学科督察组【学习目标】1、掌握圆和圆的五种位置关系中圆心距与半径之间的数量关系。2、掌握相交两圆的相关性质定理。3、初步会应用相交两圆的性质定理。【学习重点与难点】1、两圆相交,相切的概念及两圆相切的性质和判定。2、相交两圆性质定理的应用。【课前回忆】直线和圆的位置关系直线和圆的位置关系结论:【课堂探究】知识点一:圆和圆的五种位置关系rRO1O2rRO1O2rRO1O2结论:rRO1O2rRO1O2rRO1O2结论:知识点二:相交两圆的性质定理相交两圆的连心线垂直平分公共弦已知:⊙O1和⊙O2相交于A、B(如图)求证:O1O2是AB的垂直平分线1O1O2ABABABABdddCCCEFrrr思考:我们知道,圆是轴对称图形,两个圆也是组成一个轴对称图形,通过两圆圆心的直线(连心线)是它们的对称轴。由此可知,如果两个圆相切,那么切点一定在连心线上。【例题分析】例题1:已知⊙01和⊙02的半径分别为3cm和4cm,设(1)0102=8cm(2)0102=7cm(3)0102=5cm(4)0102=1cm(5)0102=0.5cm(6)01和02重合请判断⊙0和⊙02的位置关系怎样?例题2:如图⊙O的半径为5cm,点P是⊙O外一点,OP=8cm。求:(1)以P为圆心作⊙P与⊙O外切,小圆⊙P的半径是多少?(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?例题3:已知定圆0的半径是4cm,动圆P的半径是1cm。(1)设⊙P和⊙0相外切,那么点P与点O的距离是多少?点P可以在什么样的线上运动?(2)设⊙P和⊙O相内切,情况又怎样?【课堂小结】名称公共点两圆位置圆心距与半径的关系外离外切相交内切内含注:1、圆和圆的五种位置关系。2、圆心距与半径之间的数量关系是性质定理也是判定定理。3、相切两圆的连心线(经过两圆心的直线)必过切点。可用来证明三点共线。4、相交两圆的连心线垂直平分两圆的公共弦。可用来证明两线垂直或线段相等。20202TT010102020101..TT....ooPPAA....5、两圆中常用的添辅助线方法:两圆相交添两圆的公共弦两圆相切添两圆的公共切线圆与圆相交,相离,相切(把心连)【课后训练】A、基础部分1、两圆的半径分别为6cm和5cm,圆心距为3cm,则两圆的位置关系是.2、两圆的圆心距为7,半径分别为3和2,则两圆的内公切线长是.3、两圆相切,半径分别为9cm和4cm,则两圆的圆心距等于.4、已知⊙O1和⊙O2相外切,直线AB是它们的一条外公切线,切点分别是A、B,若外公切线AB和连心线的夹角是30°,两圆的圆心距是4cm,那么这两个圆的半径分别是和.5、两圆外切,半径分别为10cm和4cm,它们的公切线被外公切线截得的线段的长是.6、如图所示,两圆相交于B、D,如果BD=3,CE=6,AB=5,则AE=.7、已知两圆的半径分别为4cm和5cm,并且两圆的圆心距为10cm,那么这两个圆最多有公切线().(A)1条(B)2条(C)3条(D)4条8、两圆的外公切线成60°角,它们的圆心距为8cm,则外公切线的长为().(A)cm(B)cm(C)cm(D)cm9、设两圆的半径分别为R、r(R>r),圆心距为d,且R2+d2+r2=2Rd,则两圆的位置关系是().(A)内切(B)内切或外切(C)外切(D)相交10、已知两圆的半径分别为方程的两个根,圆心距为,则两圆的位置关系是()(A)相交(B)外离(C)外切(D)内切11、已知⊙O1和⊙O2相外切,并且⊙O1和⊙O2的半径分别为3cm和9cm,则两条外公切线的夹角是().(A)30°(B)60°(C)90°(D)120°12、两圆的圆心距为14cm,内公切线为cm,两圆的半径之差为4cm,求两圆的半径。13、已知相交于A、B两点,且的半径为12cm,的半径为4cm,求AB的长B、能力提升14、已知:如图所示,⊙O1与⊙O2相外切,CD是公切线,切⊙O1于C,切⊙O2于D,⊙O1的半径为5cm,⊙O2的半径为3cm,求:四边形O1CDO2的面积.315、已知:如图所示,⊙O1和⊙O2相交于A、B两点,直线CD过A点,交⊙O1于C,交⊙O2于D.直线BE切⊙O1于B点,交⊙O2于E点,且CD与BE延长线相交于F.求证:BF·DF=CF·EF.C、思考部分16、已知:如图所示,⊙O1与⊙O2外切于P,AD是过P点的割线,交⊙O1于A,交⊙O2于D,AC切⊙O2于C,交⊙O1于B。求证:(1)∠BPC=∠CPD.(3)CP2=BP·DP.4同步题库二7.4cm、3cm、2cm二、1.D2.B3.B4.B5.B3.提示:连结CB、BD、AB则∠BAF=∠BDF,∠BAF=∠PCB∵∠BDF=∠PCB∴P、C、B、D四点共圆4.提示:过P点作⊙O1与⊙O2的公切线MN,交BC于M,连结CD,(1)∠CPD=∠A+∠ACP,∠BPC=∠BPM+∠MPC,∵∠BPM=∠A,∠MPC=∠ACP∴∠BPC=∠A+∠ACP∴∠CPD=∠BPC(2)∵∠BCP=∠D,∠BPC=∠CPDΔ∴BPCΔ∽PCD5