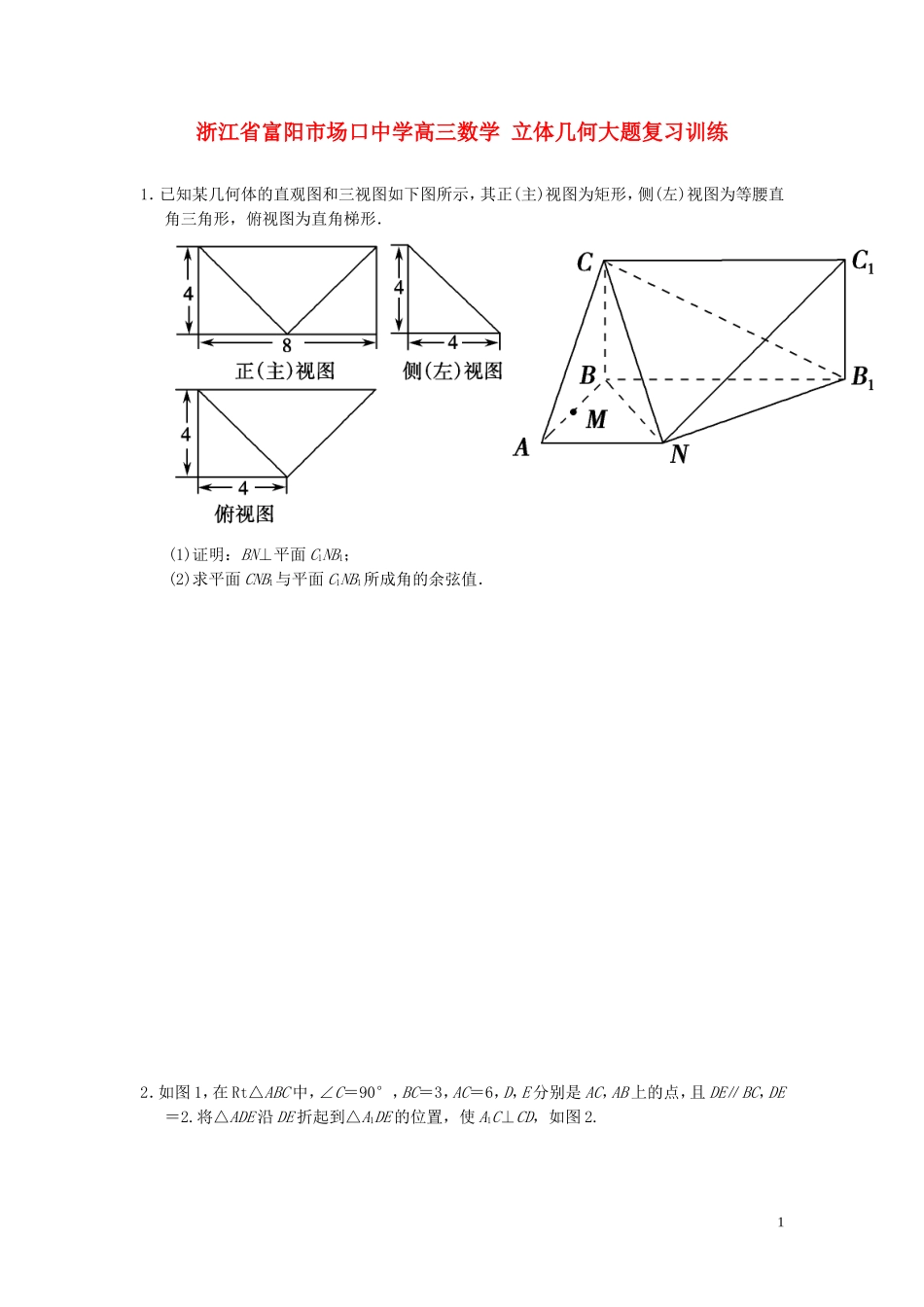
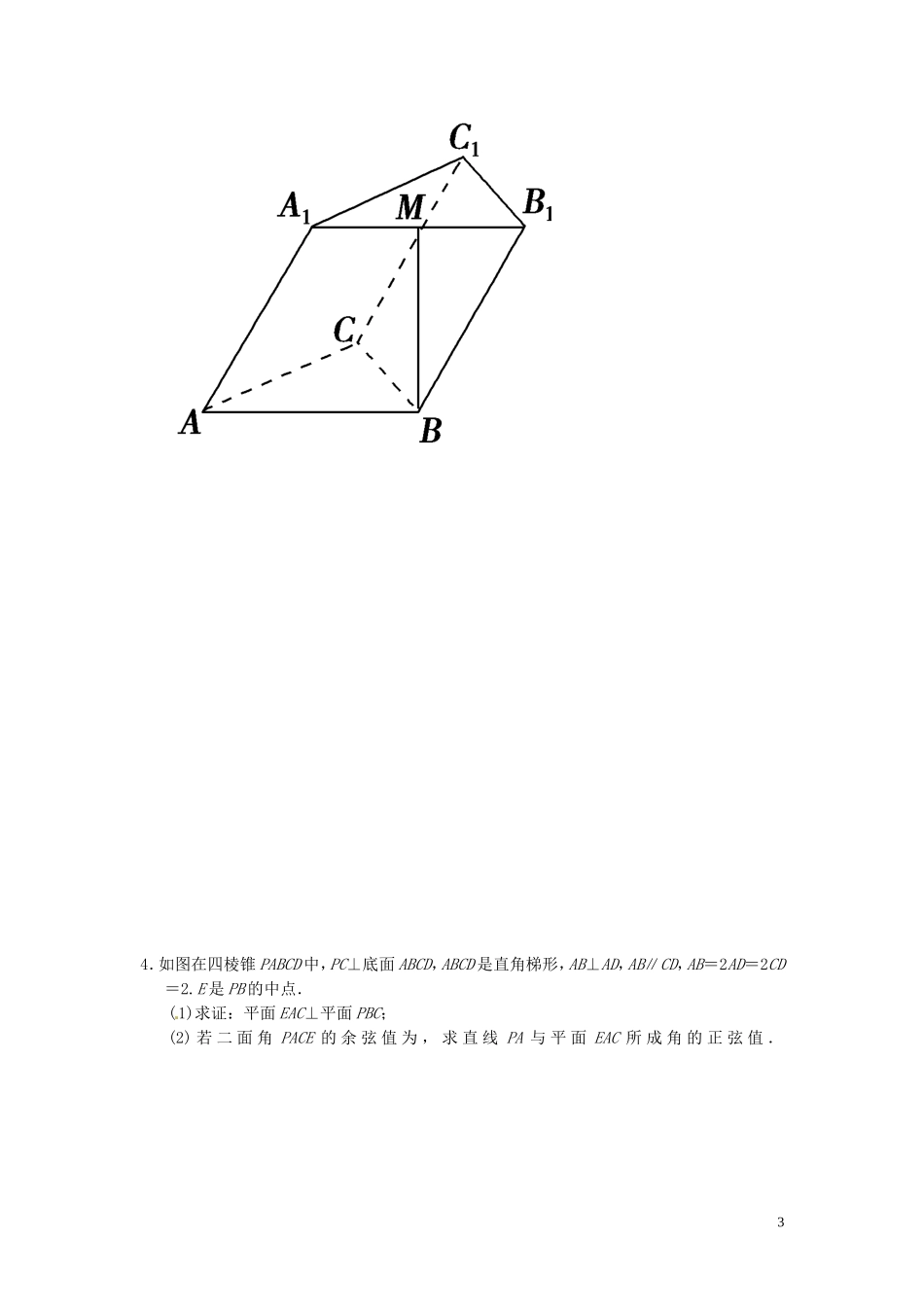
浙江省富阳市场口中学高三数学立体几何大题复习训练1.已知某几何体的直观图和三视图如下图所示,其正(主)视图为矩形,侧(左)视图为等腰直角三角形,俯视图为直角梯形.(1)证明:BN⊥平面C1NB1;(2)求平面CNB1与平面C1NB1所成角的余弦值.2.如图1,在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.1(1)求证:A1C⊥平面BCDE;(2)若M是A1D的中点,求CM与平面A1BE所成角的大小;(3)线段BC上是否存在点P,使平面A1DP与平面A1BE垂直?说明理由.3.如图,已知斜三棱柱ABCA1B1C1的底面是正三角形,侧面ABB1A1是菱形,且∠A1AB=60°,M是A1B1的中点,MB⊥AC.(1)求证:MB⊥平面ABC;(2)求二面角A1-BB1-C的余弦值.24.如图在四棱锥PABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2.E是PB的中点.(1)求证:平面EAC⊥平面PBC;(2)若二面角PACE的余弦值为,求直线PA与平面EAC所成角的正弦值.31.(1)证明∵该几何体的正(主)视图为矩形,侧(左)视图为等腰直角三角形,俯视图为直角梯形,∴BA,BC,BB1两两垂直.以BA,BB1,BC分别为x,y,z轴建立空间直角坐标系如图.则B(0,0,0),N(4,4,0),B1(0,8,0),C1(0,8,4),C(0,0,4).∴BN·NB1=(4,4,0)·(-4,4,0)=-16+16=0,BN·B1C1=(4,4,0)·(0,0,4)=0.∴NB⊥NB1,BN⊥B1C1.又NB1与B1C1相交于B1,∴BN⊥平面C1NB1.4(2)解∵BN⊥平面C1NB1,∴BN是平面C1B1N的一个法向量n1=(4,4,0),设n2=(x,y,z)为平面NCB1的一个法向量,则⇒⇒所以可取n2=(1,1,2).则cos〈n1,n2〉====.∴所求二面角CNB1C1的余弦值为.2.(1)证明因为AC⊥BC,DE∥BC,所以DE⊥AC.所以ED⊥A1D,DE⊥CD,所以DE⊥平面A1DC.所以DE⊥A1C.又因为A1C⊥CD.所以A1C⊥平面BCDE.(2)解如图,以C为坐标原点,建立空间直角坐标系Cxyz,则A1(0,0,2),D(0,2,0),M(0,1,),B(3,0,0),E(2,2,0).设平面A1BE的法向量为n=(x,y,z),则n·A1B=0,n·BE=0.又A1B=(3,0,-2),BE=(-1,2,0),所以令y=1,则x=2,z=.所以n=(2,1,).设CM与平面A1BE所成的角为θ.因为CM=(0,1,),所以sinθ=|cos〈n,CM〉|=||==.所以CM与平面A1BE所成角的大小为.(3)解线段BC上不存在点P,使平面A1DP与平面A1BE垂直,理由如下:假设这样的点P存在,设其坐标为(p,0,0),其中p∈[0,3].设平面A1DP的法向量为m=(x,y,z),则m·A1D=0,m·DP=0.又A1D=(0,2,-2),DP=(p,-2,0),所以令x=2,则y=p,z=.所以m=.平面A1DP⊥平面A1BE,当且仅当m·n=0,即4+p+p=0.解得p=-2,与p∈[0,3]矛盾.所以线段BC上不存在点P,使平面A1DP与平面A1BE垂直.3.(1)证明∵侧面ABB1A1是菱形,且∠A1AB=60°,∴△A1BB1为正三角形,又∵点M为A1B1的中点,∴BM⊥A1B1,5∵AB∥A1B1,∴BM⊥AB,由已知MB⊥AC,∴MB⊥平面ABC.(2)解如图建立空间直角坐标系,设菱形ABB1A1边长为2,得B1(0,-1,),A(0,2,0),C(,1,0),A1(0,1,).则BA1=(0,1,),BA=(0,2,0),BB1=(0,-1,),BC=(,1,0).设面ABB1A1的法向量n1=(x1,y1,z1),由n1⊥BA,n1⊥BA1得,令x1=1,得n1=(1,0,0).设面BB1C1C的法向量n2=(x2,y2,z2),由n2⊥BB1,n2⊥BC得令y2=,得n2=(-1,,1),得cos〈n1,n2〉===-.又二面角A1BB1C为锐角,所以所求二面角的余弦值为.4.(1)证明∵PC⊥平面ABCD,AC⊂平面ABCD,∴AC⊥PC,∵AB=2,AD=CD=1,∴AC=BC=,∴AC2+BC2=AB2,∴AC⊥BC,又BC∩PC=C,∴AC⊥平面PBC,∵AC⊂平面EAC,∴平面EAC⊥平面PBC.(2)解如图,以C为原点,DA、CD、CP分别为x轴、y轴、z轴正向,建立空间直角坐标系,则C(0,0,0),A(1,1,0),B(1,-1,0).设P(0,0,a)(a>0),则E,-,,CA=(1,1,0),CP=(0,0,a),CE=,-,,取m=(1,-1,0),则m·CA=m·CP=0,m为面PAC的法向量.设n=(x,y,z)为面EAC的法向量,则n·CA=n·CE=0,即取x=a,y=-a,z=-2,则n=(a,-a,-2),依题意,|cos〈m,n〉|===,则a=2.于是n=(2,-2,-2),PA=(1,1,-2).设直线PA与平面EAC所成角为θ,则sinθ=|cos〈PA,n〉|==,即直线PA与平面EAC所成角的正弦值为.67