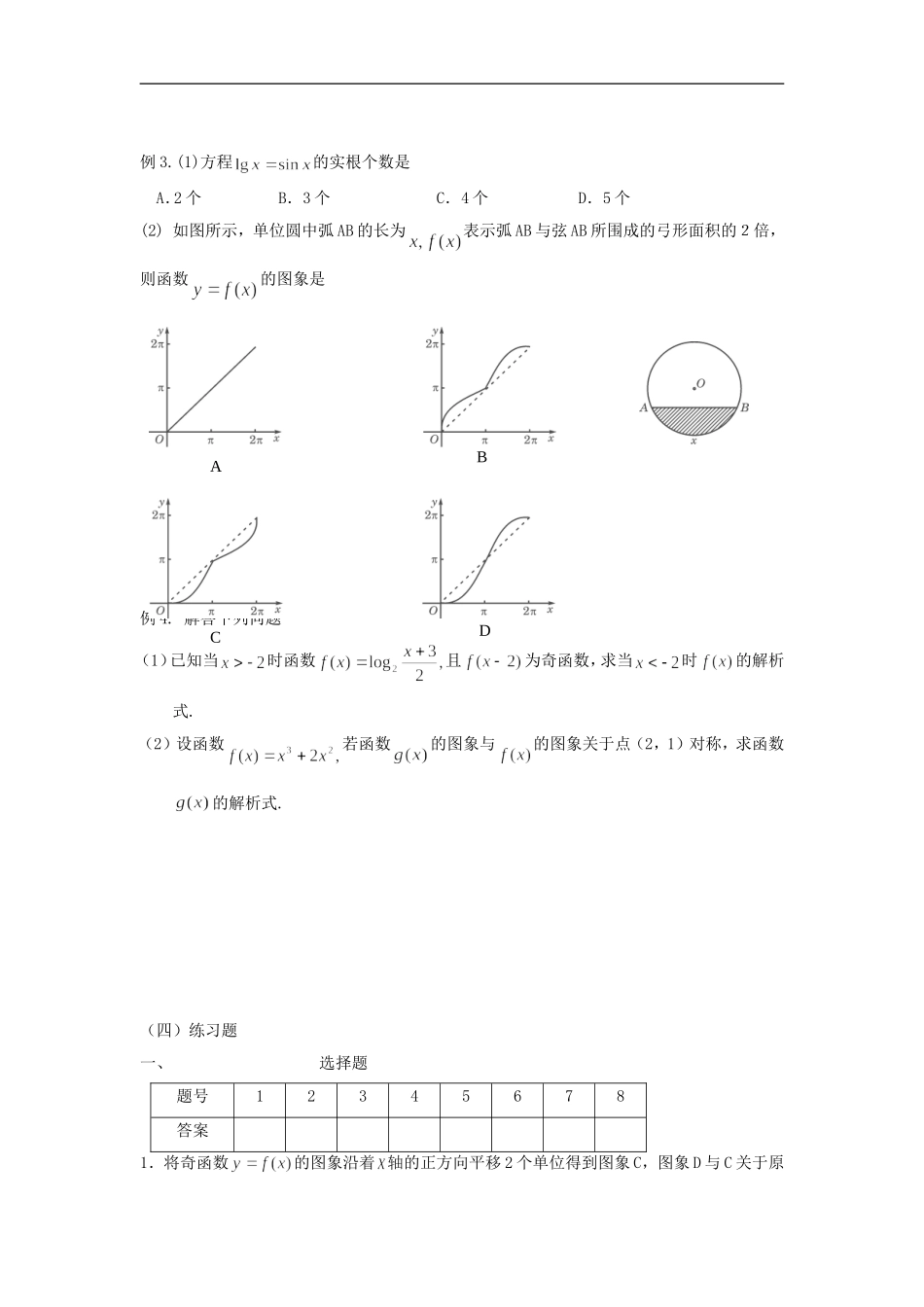
(六)函数的图象(一)知识归纳1.函数图象作图方法(1)描点法:列表、描点(注意关键点:如图象与、轴的交点,极值点,对称轴,渐近线,等等)、连线;(2)利用基本函数图象变换。2.图象变换(由一个图象得到另一个图象):平移变换、对称变换和伸缩变换等。(1)平移变换①水平平移:函数的图象可以把函数的图象沿轴方向向左或向右平移个单位即可得到;②竖直平移:函数的图象可以把函数的图象沿轴方向向上或向下平移个单位即可得到.(2)对称变换①函数的图象可以将函数的图象关于轴对称即可得到;②函数的图象可以将函数的图象关于轴对称即可得到;③函数的图象可以将函数的图象关于原点对称即可得到;*④函数(这是的反函数的符号)的图象可以将函数的图象关于直线对称得到.(3)翻折变换①函数的图象可以将函数的图象的轴下方部分沿轴翻折到轴上方,去掉原轴下方部分,并保留的轴上方部分即可得到;②函数的图象可以将函数的图象右边沿轴翻折到轴左边替代原轴左边部分并保留在轴右边部分即可得到.(4)伸缩变换①函数的图象可以将函数的图象中的每一点横坐标不变纵坐标伸长或压缩()为原来的倍得到;②函数的图象可以将函数的图象中的每一点纵坐标不变横坐标伸长或压缩()为原来的倍得到.3.函数图象的对称性:对于函数,若对定义域内的任意都有①(或,则的图象关于直线对称;②(或,,则的图象关于点对称.(二)学习要点1.熟练掌握基本初等函数(如正、反比例函数,一次、二次函数,指数、对数函数,幂函数,三角函数)的图象2.作函数图象的一般步骤:(1)求出函数的定义域;(2)化简函数式;(3)讨论函数的性质;(4)利用描点法或图象变换作图。3.判断函数图象的方法判断函数图象是高三考试中经常出现的内容,大多属于简单题,值得重视。常用方法有:(1)取点(描点)(2)考虑函数的定义域、值域、奇偶性、单调性、变化趋势、对称性等方面(3)利用平移(4)利用基本形状4.应用:利用函数图象解决有关问题,即“数形结合”思想解答问题或帮助分析问题。(三)例题讲评例1.将下列变换的结果填在横线上(1)将函数的图象向右平移2个单位,得到函数的图象;(2)将函数的图象向右平移3个单位,得到函数的图象;(3)将函数的图象作变换,得到函数的图象;(4)将函数的图象向左平移2个单位,得到函数的图象;(5)将函数的图象各点的横坐标伸长到原来的3倍(纵坐标不变)得到函数___________________的图象.例2.作出下列函数图象(1);(2);(3);例3.(1)方程的实根个数是A.2个B.3个C.4个D.5个(2)如图所示,单位圆中弧AB的长为表示弧AB与弦AB所围成的弓形面积的2倍,则函数的图象是例4.解答下列问题(1)已知当时函数且为奇函数,求当时的解析式.(2)设函数若函数的图象与的图象关于点(2,1)对称,求函数的解析式.(四)练习题一、选择题题号12345678答案1.将奇函数的图象沿着轴的正方向平移2个单位得到图象C,图象D与C关于原ADCB点对称,则D对应的函数是A.B.C.D.2.函数的图象大致是3.函数的图象,可由的图象经过下述变换得到A.向左平移3个单位B.向右平移3个单位C.向左平移6个单位D.向右平移6个单位4.设函数与函数的图象如右图所示,则函数的图象可能是下面的5.若函数的图象过两点(-1,0)和(0,1),则A.=2,b=2B.=,b=2C.=2,b=1D.=,b=6.如图,点P在边长的1的正方形的边上运动,设M是CD边的中点,当P沿A→B→C→M运动时,以点P经过的路程为自变量,的面积为,则函数的图象大致是7.函数的图象A.与的图象关于y轴对称B.与的图象关于坐标原点对称C.与的图象关于y轴对称D.与的图象关于坐标原点对称8.已知函数的反函数是,则函数的图象是v二、填空题9.函数的图象与的图象关于直线对称,则的表达式是10.已知函数给出下列四个命题:①函数的图象关于点(1,1)对称;②函数的图象关于直线对称;③函数在定义域内单调递减;④将函数图象向左平移一个单位,再向下平移一个单位后与函数重合.则其中正确命题的序号是11.若直线与函数的图象有两个公共点,则的取值范围是____.12.设函数的定义域为R,则下列命题中:①若为偶函数,则...