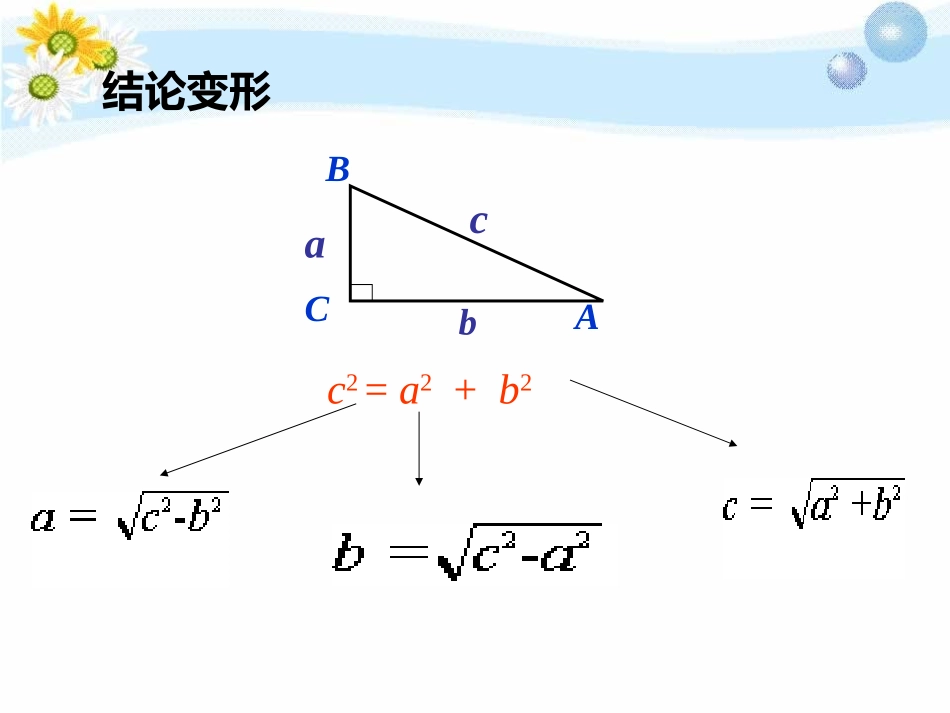
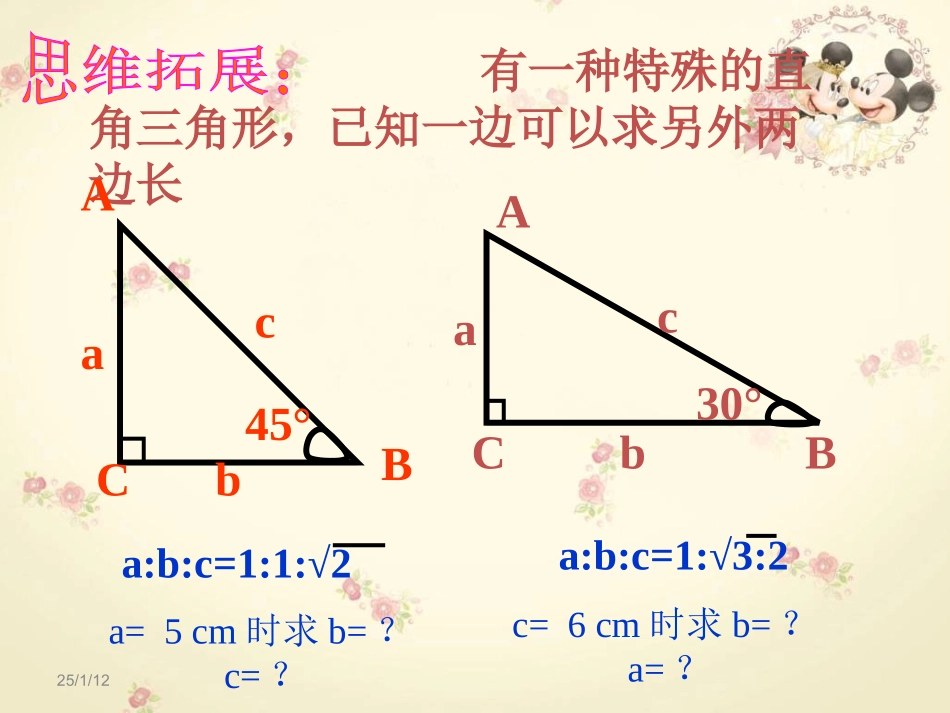
结论变形c2=a2+b2abcABC25/1/12有一种特殊的直角三角形,已知一边可以求另外两边长ACBbac45°ACBbac30°a:b:c=1:1:√2a:b:c=1:√3:2a=5cm时求b=?c=?c=6cm时求b=?a=?勾股小常识:勾股数1、基本勾股数如:大家一定要熟记2、如果a,b,c是一组勾股数,则ka、kb、kc(k为正整数)也是一组勾股数,如:6、8、10;9、12、1510、24、26;15、36、39112、、132、、345、、51213、、72425、、例1、已知:在Rt△ABC中,∠C=90°,CD⊥AB于D,∠A=60°,CD=,求线段AB的长.3ACBD变式训练:△ABC中,AB=10,AC=17,BC边上的高线AD=8,求线段BC的长和△ABC的面积.ABC17108D10178615621或9SABC△=84或36当题中没有给出图形时,应考虑图形的形状是否确定,如果不确定,就需要分类讨论。15例2、在△ABC中,∠C=30°,AC=4cm,AB=3cm,求BC的长.ACBD勾股定理在非直角三角形中的应用:见特殊角作高构造直角三角形.变式1、在△ABC中,∠B=120°,BC=4cm,AB=6cm,求AC的长.ABCD变式2、在等腰△ABC中,AB=AC=13cm,BC=10cm,求△ABC的面积和AC边上的高.ABCABCABCABCDABCABCE两个直角三角形中,如果有一条公共边,可利用勾股定理建立方程求解.变式3、已知:如图,△ABC中,AB=26,BC=25,AC=17,求△ABC的面积.BCA方程思想:两个直角三角形中,如果有一条公共边,可利用勾股定理建立方程求解.D例3、已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2.求四边形ABCD的面积.ACBDFEACBDMACDBABCOxy变式训练:如图,在平面直角坐标系中,点C的坐标为(0,4),∠B=90°,∠BCO=60°,AB=2,求点B的坐标.例4、如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,AC=6cm,BC=8cm,(1)求线段CD的长;(2)求△ABD的面积.xx8-x664方程思想:直角三角形中,已知一条边,以及另外两条边的数量关系时,可利用勾股定理建立方程求解.DCBAE810DOBAExyDOBAEDOBADOBAExy变式练习:如图,在直角坐标系中,△ABO的顶点A为(0,6),B为(8,0),AD平分∠BAO交x轴于点D,DE⊥AB于E.(1)求△ABD的面积;(2)求点E的坐标.例3:在我国古代数学著作《九章算术》中记载了一道有趣的问题这个问题意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,问这个水池的深度和这根芦苇的长度各是多少?DABC解:设水池的深度AC为X米,则芦苇高AD为(X+1)米.根据题意得:BC2+AC2=AB2∴52+X2=(X+1)225+X2=X2+2X+1X=12∴X+1=12+1=13(米)答:水池的深度为12米,芦苇高为13米.如图,小颍同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AC=10cm,BC=6cm,你能求出CE的长吗?ECABDx10-x6练习5(1)已知直角三角形两边的长分别是3cm和6cm,则第三边的长是.(2)△ABC中,AB=AC=2,BD是AC边上的高,且BD与AB的夹角为300,求CD的长.DCABDCAB25/1/12分类思想1.直角三角形中,已知两边长,求第三边时,应分类讨论。2.当已知条件中没有给出图形时,应认真读句画图,避免遗漏另一种情况。例7(1)直角三角形中,斜边与一直角边相差8,另一直角边为12,求斜边的长.例7(2)如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长.EDCBAxx8-x664方程思想:直角三角形中,已知一直角边,以及另一直角边和斜边的等量关系,可建立方程求解.例2:如图,铁路上A,B两点相距25km,C,D为两庄,DAAB⊥于A,CBAB⊥于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?CAEBDx25-x解:设AE=xkm,根据勾股定理,得AD2+AE2=DE2BC2+BE2=CE2又∵DE=CE∴AD2+AE2=BC2+BE2即:152+x2=102+(25-x)2答:E站应建在离A站10km处。∴X=10则BE=(25-x)km1510