空间解析几何简介VIP免费

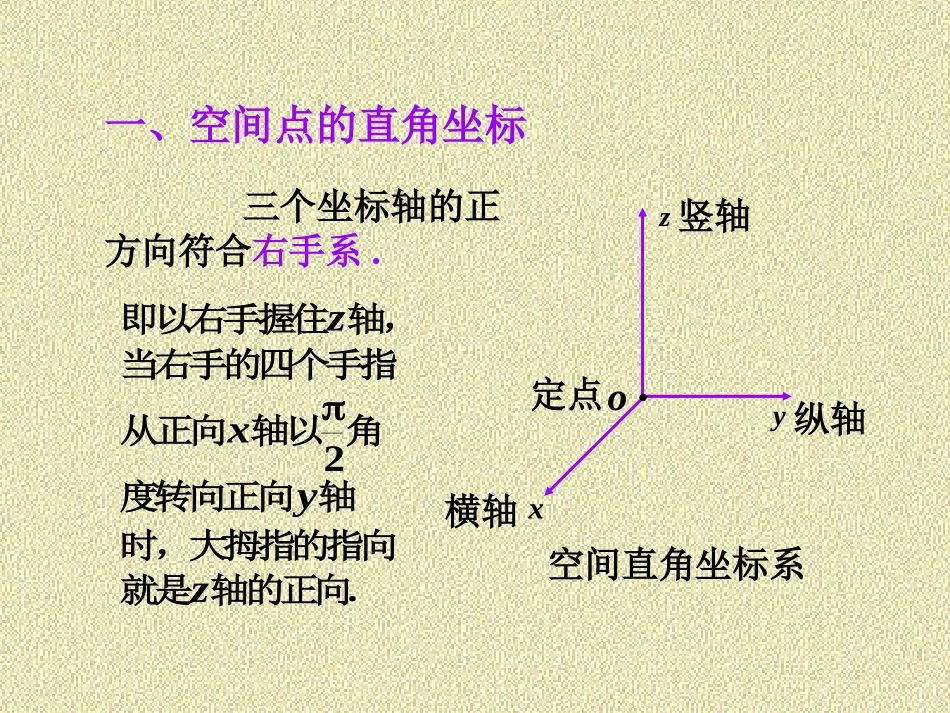
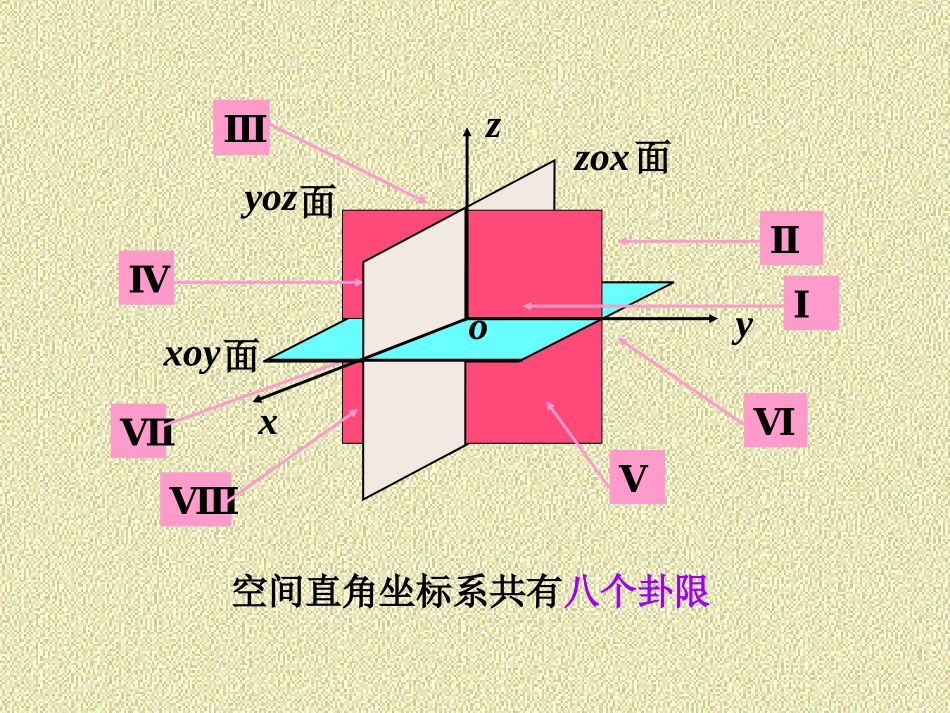
第一讲空间解析几何简介•内容提要1.空间直角坐标系;2.空间两点之间的距离;3.空间曲面、空间曲线常见的二次曲面;4.空间曲线在坐标面上的投影。•教学要求1.初步建立空间的概念，理解空间直角坐标系；2.理解曲面及其方程的概念；3.掌握几种特殊曲面的方程及其图形；4.理解空间直线及其方程概念；5.掌握几种空间直线方程的形式特点；6.理解空间曲线及其方程概念；7.掌握几种空间曲线及其方程形式特点。x横轴y纵轴z竖轴定点o空间直角坐标系三个坐标轴的正方向符合右手系.即以右手握住z轴，当右手的四个手指从正向x轴以2角度转向正向y轴时，大拇指的指向就是z轴的正向.一、空间点的直角坐标Ⅶxyozxoy面yoz面zox面空间直角坐标系共有八个卦限ⅠⅡⅢⅣⅤⅥⅧ空间的点有序数组),,(zyx11特殊点的表示:)0,0,0(O),,(zyxMxyzo)0,0,(xP)0,,0(yQ),0,0(zR)0,,(yxA),,0(zyB),,(zoxC坐标轴上的点,P,Q,R坐标面上的点,A,B,C设),,(1111zyxM、),,(2222zyxM为空间两点xyzo1MPNQR2M?21MMd在直角21NMM及直角PNM1中，使用勾股定理知,222212NMPNPMd二、空间两点间的距离,121xxPM,12yyPN,122zzNM22221NMPNPMd.21221221221zzyyxxMM空间两点间距离公式特殊地：若两点分别为,),,(zyxM)0,0,0(OOMd.222zyxxyzo1MPNQR2M解221MM,14)12()31()47(222232MM,6)23()12()75(222213MM,6)31()23()54(22232MM,13MM原结论成立.例1求证以)1,3,4(1M、)2,1,7(2M、)3,2,5(3M三点为顶点的三角形是一个等腰三角形.例2设P在x轴上，它到)3,2,0(1P的距离为到点)1,1,0(2P的距离的两倍，求点P的坐标.解设P点坐标为),0,0,(x因为P在x轴上，1PP22232x,112x2PP22211x,22x1PP,22PP112x222x,1x所求点为).0,0,1(),0,0,1(曲面方程的定义：（1）曲面S上任一点的坐标都满足方程；（2）不在曲面S上的点的坐标都不满足方程；那么，方程0),,(zyxF就叫做曲面S的方程，而曲面S就叫做方程的图形．曲面的实例：三、空间曲面水桶的表面、台灯的罩子面等．曲面在空间解析几何中被看成是点的几何轨迹．如果曲面S与三元方程0),,(zyxF有下述关系：曲面方程的概念以下给出几例常见的曲面.例1建立球心在点),,(0000zyxM、半径为R的球面方程.解设),,(zyxM是球面上任一点，RMM||0根据题意有Rzzyyxx2020202202020Rzzyyxx所求方程为特殊地：球心在原点时方程为2222Rzyx例2求与原点O及)4,3,2(0M的距离之比为2:1的点的全体所组成的曲面方程.解设),,(zyxM是曲面上任一点，,21||||0MMMO根据题意有,21432222222zyxzyx.911634132222zyx所求方程为例3已知)3,2,1(A，)4,1,2(B，求线段AB的垂直平分面的方程.设),,(zyxM是所求平面上任一点，根据题意有|,|||MBMA222321zyx,412222zyx化简得所求方程.07262zyx解zxyo1)2()1(22yxz根据题意有1z用平面cz去截图形得圆：)1(1)2()1(22ccyx当平面cz上下移动时，得到一系列圆圆心在),2,1(c，半径为c1半径随c的增大而增大.c图形上不封顶，下封底．解例4方程的图形是怎样的？以上几例表明研究空间曲面有两个基本问题：（讨论旋转曲面）（讨论柱面、二次曲面）（2）已知坐标间的关系式，研究曲面形状．（1）已知曲面作为点的轨迹时，求曲面方程．四、空间曲线0),,(0),,(zyxGzyxF空间曲线的一般方程曲线上的点都满足方程，满足方程的点都在曲线上，不在曲线上的点不能同时满足两个方程.xozy1S2SC空间曲线C可看作空间两曲面的交线.特点：例1方程组表示怎样的曲线？6332122zyxyx解122yx表示圆柱面，6332zyx表示平面，6332122zyxyx交线为椭圆.五、常见曲面ozyx（一）椭球面1222222czbyax椭球面与三个坐标面的交线：,012222ycz...