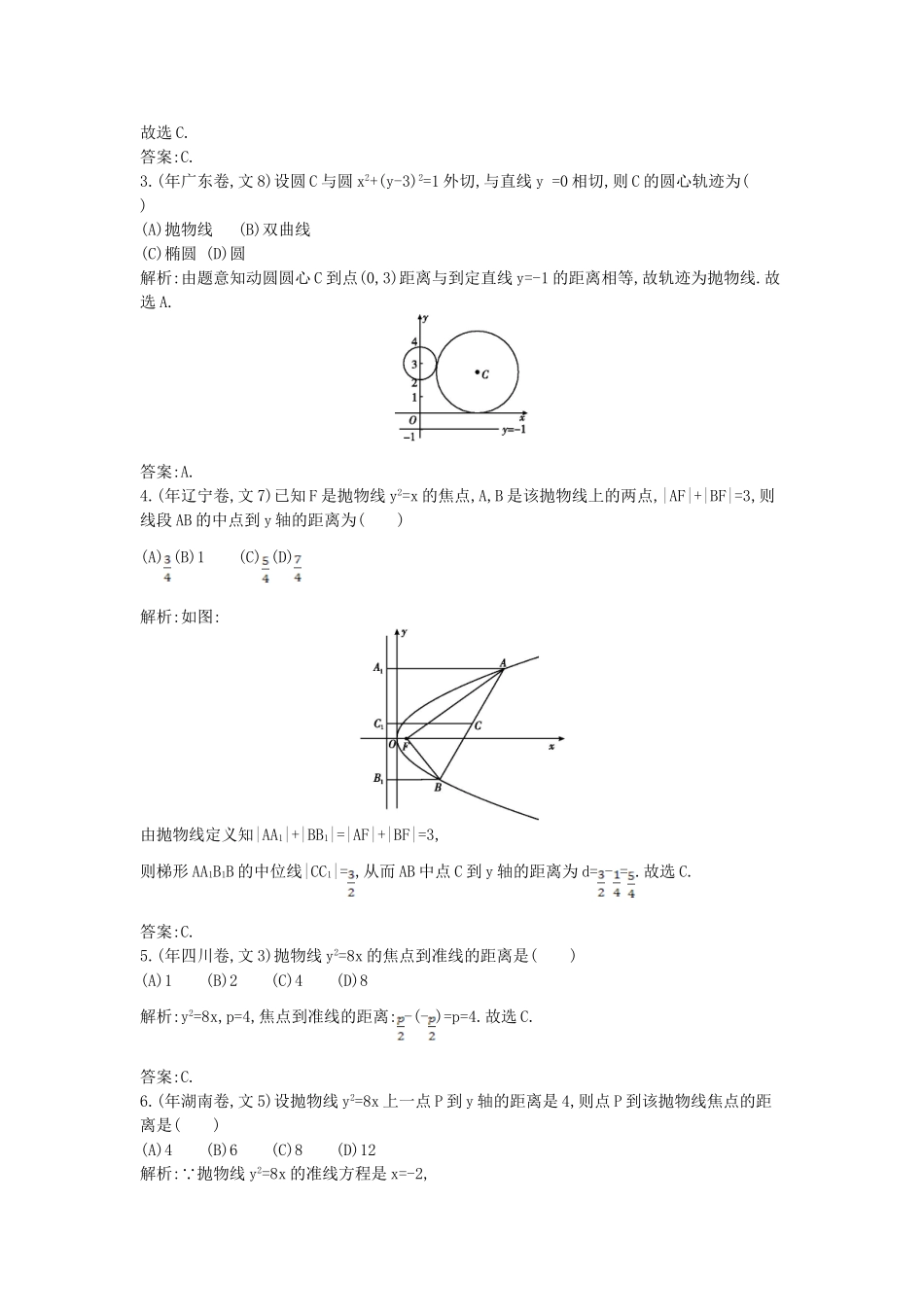
第五节抛物线抛物线的定义及其应用考向聚焦高考热点,主要考查与抛物线的定义有关的最值、距离、轨迹等问题,单独命题一般以选择题、填空题形式出现;大多渗透于解答题中,难度中档,所占分值4~5分备考指津训练题型:(1)与抛物线有关的轨迹问题,注意分析问题的能力的训练;(2)最值问题,注意转化与化归思想的培养.(3)距离问题,注意解题方法的训练1.(年四川卷,文9,5分)已知抛物线关于x轴对称,它的顶点在坐标原点O,并且经过点M(2,y0).若点M到该抛物线焦点的距离为3,则|OM|等于()(A)2(B)2(C)4(D)2解析:因为抛物线的对称轴是x轴,且过点M(2,y0),点M到焦点的距离为3,所以p=2,抛物线的方程为y2=4x,|OM|===2,故选B.答案:B.2.(年新课标全国卷,文9)已知直线l过抛物线C的焦点,且与C的对称轴垂直,l与C交于A,B两点,|AB|=12,P为C的准线上一点,则△ABP的面积为()(A)18(B)24(C)36(D)48解析:设抛物线方程为y2=2px(p>0),F为抛物线焦点,则直线l垂直于x轴,AF==6,∴△ABP的边AB上的高h=6,∴S△ABP=×12×6=36.故选C.答案:C.3.(年广东卷,文8)设圆C与圆x2+(y-3)2=1外切,与直线y=0相切,则C的圆心轨迹为()(A)抛物线(B)双曲线(C)椭圆(D)圆解析:由题意知动圆圆心C到点(0,3)距离与到定直线y=-1的距离相等,故轨迹为抛物线.故选A.答案:A.4.(年辽宁卷,文7)已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为()(A)(B)1(C)(D)解析:如图:由抛物线定义知|AA1|+|BB1|=|AF|+|BF|=3,则梯形AA1B1B的中位线|CC1|=,从而AB中点C到y轴的距离为d=-=.故选C.答案:C.5.(年四川卷,文3)抛物线y2=8x的焦点到准线的距离是()(A)1(B)2(C)4(D)8解析:y2=8x,p=4,焦点到准线的距离:-(-)=p=4.故选C.答案:C.6.(年湖南卷,文5)设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是()(A)4(B)6(C)8(D)12解析: 抛物线y2=8x的准线方程是x=-2,且抛物线上的点到焦点的距离等于到准线的距离.∴由题意知,点P到焦点的距离等于4-(-2)=6.故选B.答案:B.7.(年安徽卷,文14,5分)过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点.若|AF|=3,则|BF|=.解析:抛物线焦点坐标(1,0),准线方程x=-1,由|AF|=3知点A(xA,yA)到准线距离为3,所以xA=2,得yA=±2,不妨设yA=2.因此直线AB的方程为y=2(x-1)代入抛物线方程8(x-1)2=4x,于是(2x-1)(x-2)=0,所以xB=,(xB=2舍去),于是点B到准线距离为,所以|BF|=.答案:8.(年陕西卷,文14,5分)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽米.解析:先以拱顶为原点,建立直角坐标系,设水面和拱桥交点A(2,-2),则抛物线方程为x2=-2py,代入得22=-2p×(-2),∴2p=2,x2=-2y,当水面下降1米时,水面和拱桥的交点记作B(a,-3)则代入抛物线方程得:a=,因此水面宽2米.答案:29.(年上海卷,文8)动点P到点F(2,0)的距离与它到直线x+2=0的距离相等,则点P的轨迹方程为.解析:由抛物线定义得P点的轨迹为焦点在x轴上的抛物线,又=2,∴p=4,∴y2=8x.答案:y2=8x抛物线的标准方程与几何性质考向聚焦高考热点内容,主要从两个方面进行考查:(1)给出抛物线方程研究其几何性质;(2)利用几何性质求抛物线方程,一般为选择题、填空题,难度不大,所占分值5分左右10.(年陕西卷,文2)设抛物线的顶点在原点,准线方程为x=-2,则抛物线的方程是()(A)y2=-8x(B)y2=-4x(C)y2=8x(D)y2=4x解析:由抛物线准线方程为x=-2知抛物线方程为y2=8x.故选C.答案:C.11.(年山东卷,文9)设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是()(A)(0,2)(B)[0,2](C)(2,+∞)(D)[2,+∞)解析:设圆的半径为r,因为F(0,2)是圆心,抛物线C的准线方程为y=-2.圆与准线相切时半径为4.若圆与准线相交则r>4.又因为点M(x0,y0)为抛物线x2=8y上一点,所以有=8y0.又点M(x0,y0)在圆x2+(y-2)2=r2上.所以+(y0-2)2=r2>16,所以8y0+(y0-2)2>16,即有+4y0-12>0,解得y0>2或y0<-6(舍),∴y0>2.故选C.答案:C.12.(年湖北卷,文4)将两个顶点在抛物线y2=2px(p>0)上,另一个顶点是此抛物线焦点的正三角形个数记为n,则()(A)n=0(B)n=1(C)n=2(D)n≥3解析:设抛物线上点A(,y1),B(,y2),且y1≠y2,焦点F(,0),由|AF|=|BF|得(-)(...