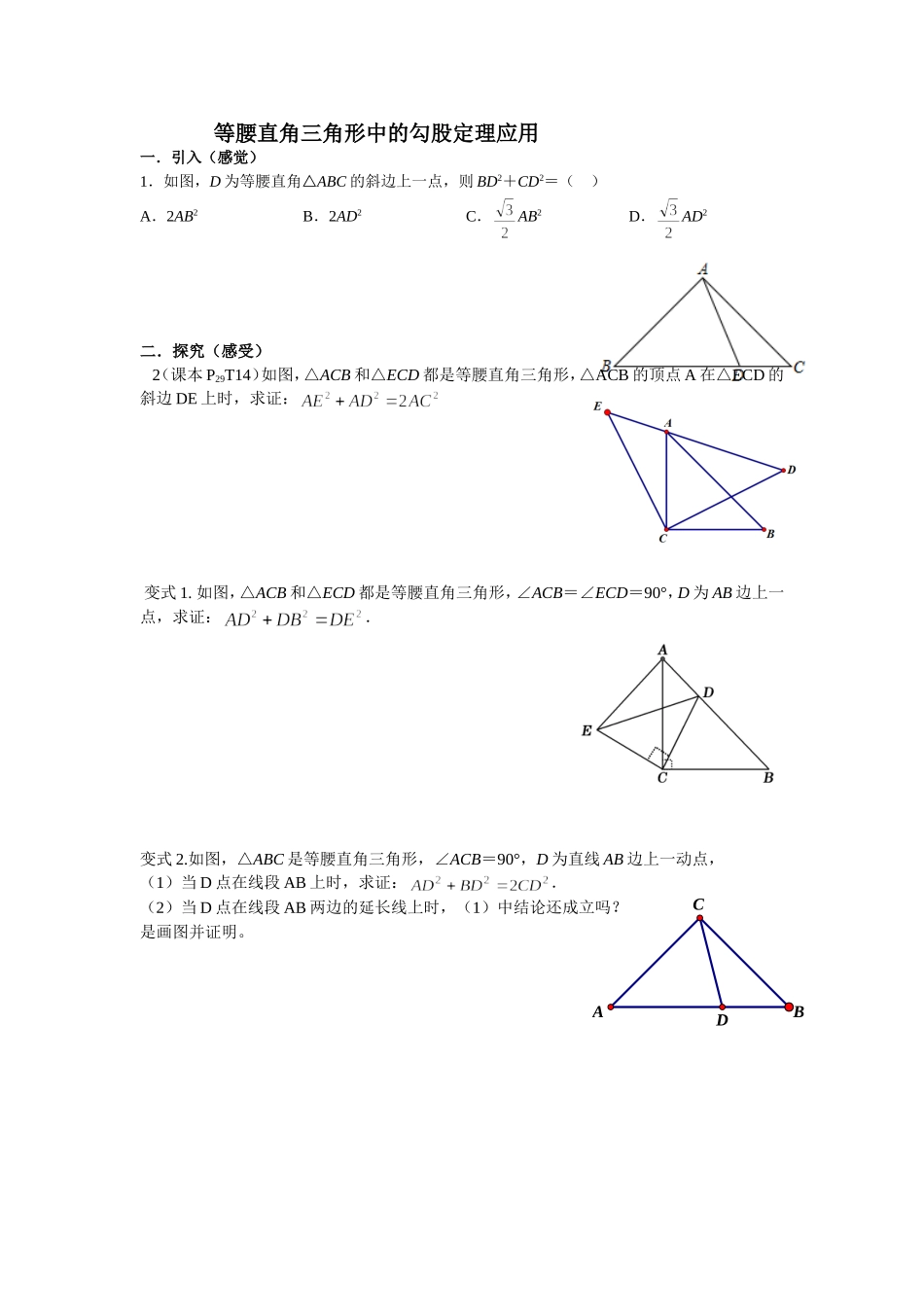
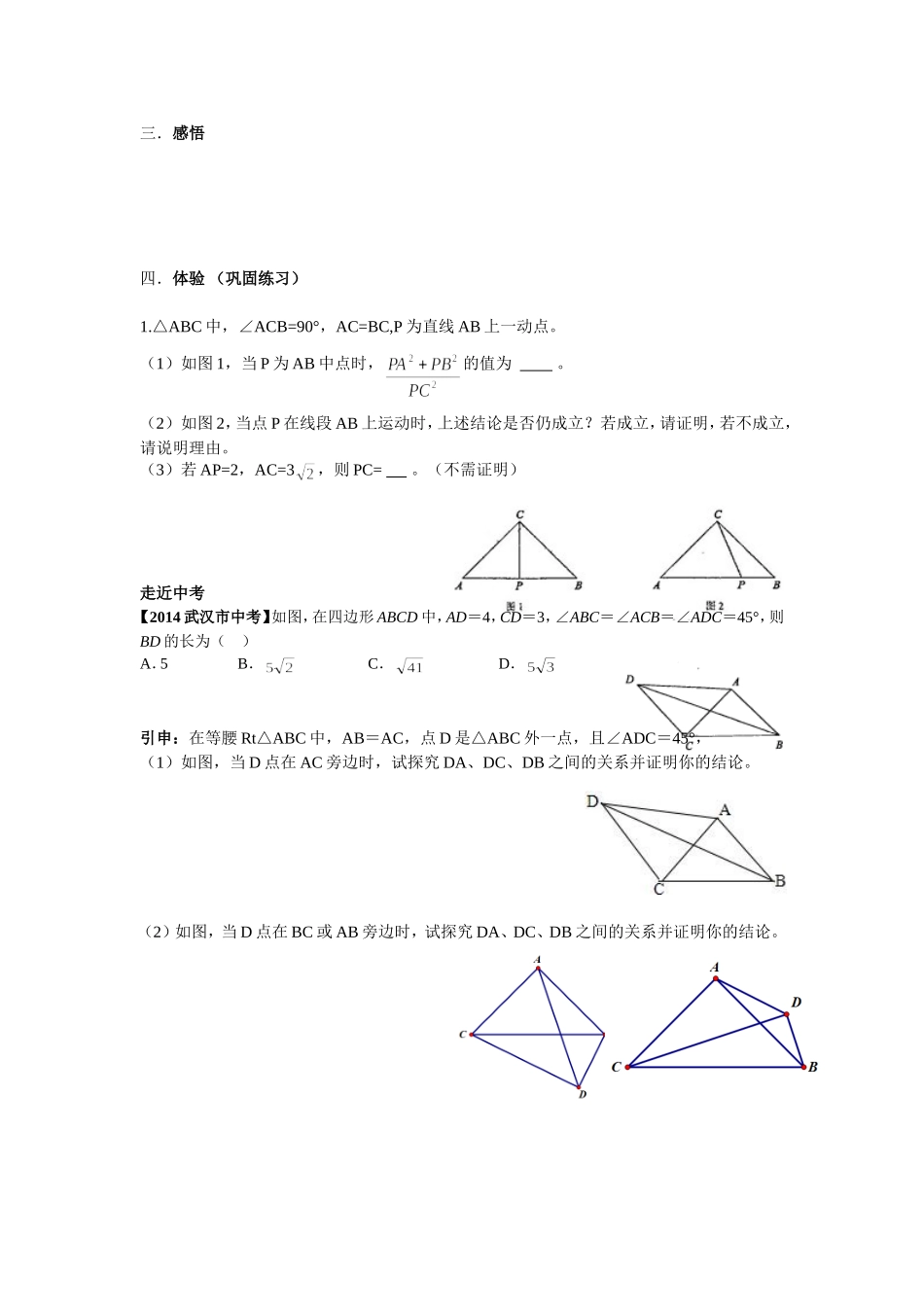
BCAD等腰直角三角形中的勾股定理应用一.引入(感觉)1.如图,D为等腰直角△ABC的斜边上一点,则BD2+CD2=()A.2AB2B.2AD2C.AB2D.AD2二.探究(感受)2(课本P29T14)如图,△ACB和△ECD都是等腰直角三角形,△ACB的顶点A在△ECD的斜边DE上时,求证:变式1.如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:.变式2.如图,△ABC是等腰直角三角形,∠ACB=90°,D为直线AB边上一动点,(1)当D点在线段AB上时,求证:.(2)当D点在线段AB两边的延长线上时,(1)中结论还成立吗?是画图并证明。三.感悟四.体验(巩固练习)1.△ABC中,∠ACB=90°,AC=BC,P为直线AB上一动点。(1)如图1,当P为AB中点时,的值为。(2)如图2,当点P在线段AB上运动时,上述结论是否仍成立?若成立,请证明,若不成立,请说明理由。(3)若AP=2,AC=3,则PC=。(不需证明)走近中考【2014武汉市中考】如图,在四边形ABCD中,AD=4,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为()A.5B.C.D.引申:在等腰Rt△ABC中,AB=AC,点D是△ABC外一点,且∠ADC=45°,(1)如图,当D点在AC旁边时,试探究DA、DC、DB之间的关系并证明你的结论。(2)如图,当D点在BC或AB旁边时,试探究DA、DC、DB之间的关系并证明你的结论。