课题学习教育储蓄VIP免费

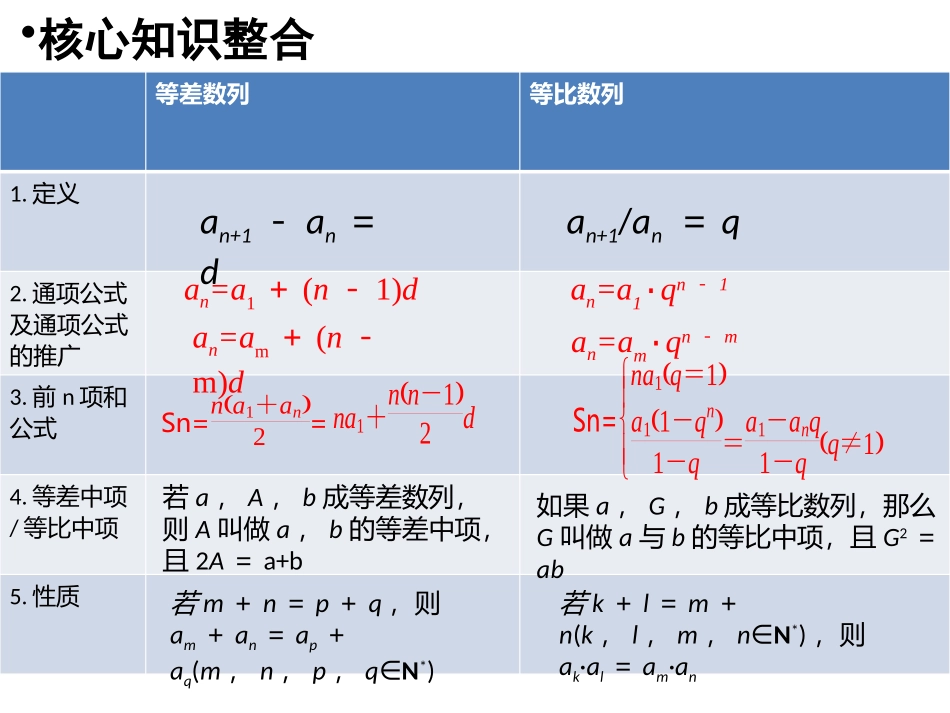
等差、等比数列复习课（第一课时）梧州八中闭春柳2018.4.16等差数列等比数列1.定义2.通项公式及通项公式的推广3.前n项和公式4.等差中项/等比中项5.性质an+1－an＝dan+1/an＝qan=a1＋(n－1)dan=am＋(n－m)dan=a1·qn－1an=am·qn－mSn=na1＋an2=na1＋nn－12dSn=na1q＝1a11－qn1－q＝a1－anq1－qq≠1若a，A，b成等差数列，则A叫做a，b的等差中项，且2A＝a+b如果a，G，b成等比数列，那么G叫做a与b的等比中项，且G2＝ab若m＋n＝p＋q，则am＋an＝ap＋aq(m，n，p，q∈N*)若k＋l＝m＋n(k，l，m，n∈N*)，则ak·al＝am·an•核心知识整合•命题方向1等差、等比数列的基本运算例1（1）（P109）已知在等差数列{an}中，a2=7，a4=15，则前10项和S10=（2）（P118）在等比数列{an}中，若a4-a2=6，a5-a1=15，则a3=知三求二，体现方程的思想•跟踪训练1．(2017·全国卷Ⅰ，4)记Sn为等差数列{an}的前n项和．若a4＋a5＝24，S6＝48，则{an}的公差为()A．1B．2C．4D．81.[解析]设{an}的公差为d，则由a4＋a5＝24，S6＝48，得a1＋3d＋a1＋4d＝24，6a1＋6×52d＝48，解得d＝4．故选C．2．(2017·江苏卷，9)等比数列{an}的各项均为实数，其前n项和为Sn.已知S3＝74，S6＝634，则a8＝__________.2.[解析]显然q≠1设{an}的首项为a1，公比为q，则a11－q31－q＝74，a11－q61－q＝634，解得a1＝14，q＝2，所以a8＝14×27＝25＝32．•命题方向2等差、等比数列的基本性质及应用例2，（1）在等差数列{an}中，若a3+a4+a5+a6+a7=25,则a2+a8=（2）在等差数列{an}中，已知a1=20，前n项和为Sn，且S10=S15，求当n取何值时，Sn取得最大值，并求出它的最大值项的性质①函数法②邻项变号法2．(2017·全国卷Ⅲ，9)等差数列{an}的首项为1，公差不为0.若a2，a3，a6成等比数列，则{an}的前6项和为()A．－24B．－3C．3D．8•跟踪训练1.(2015·课标全国Ⅱ)设Sn是等差数列{an}的前n项和，若a1＋a3＋a5＝3，则S5等于()A．5B．7C．9D．113.已知等差数列{an}的首项a1＝20，公差d＝－2，则前n项和Sn的最大值为________．AA110•命题方向3等差、等比数列的判断与证明例3(2016·全国卷Ⅲ，17)已知数列{an}的前n项和Sn＝1＋λan.其中λ≠0.(1)证明{an}是等比数列，并求其通项公式；(2)若S5＝3132，求λ．[解析](1)由题意得a1＝S1＝1＋λa1，故λ≠1，a1＝11－λ，a1≠0．由Sn＝1＋λan，Sn＋1＝1＋λan＋1得an＋1＝λan＋1－λan，即an＋1(λ－1)＝λan．由a1≠0，λ≠0且λ≠1得an≠0，所以an＋1an＝λλ－1．因此{an}是首项为11－λ，公比为λλ－1的等比数列，于是an＝11－λ(λλ－1)n－1．(2)由(1)得Sn＝1－(λ1－λ)n.由S5＝3132得1－(λλ－1)5＝3132，即(λλ－1)5＝132.解得λ＝－1．利用定义(2017·全国卷Ⅰ，17)记Sn为等比数列{an}的前n项和．已知S2＝2，S3＝－6.(1)求{an}的通项公式；(2)求Sn，并判断Sn＋1，Sn，Sn＋2是否成等差数列．[解析](1)设{an}的公比为q.由题设可得a11＋q＝2，a11＋q＋q2＝－6.解得q＝－2，a1＝－2．故{an}的通项公式为an＝(－2)n．(2)由(1)可得Sn＝a11－qn1－q＝－23＋(－1)n2n＋13．由于Sn＋2＋Sn＋1＝－43＋(－1)n2n＋3－2n＋23＝2[－23＋(－1)n2n＋13]＝2Sn，故Sn＋1，Sn，Sn＋2成等差数列．•跟踪训练等差数列等比数列1.定义2.通项公式及通项公式的推广3.前n项和公式4.等差中项/等比中项5.性质an+1－an＝dan+1/an＝qan=a1＋(n－1)dan=am＋(n－m)dan=a1·qn－1an=am·qn－mSn=na1＋an2=na1＋nn－12dSn=na1q＝1a11－qn1－q＝a1－anq1－qq≠1若a，A，b成等差数列，则A叫做a，b的等差中项，且2A＝a+b如果a，G，b成等比数列，那么G叫做a与b的等比中项，且G2＝ab若m＋n＝p＋q，则am＋an＝ap＋aq(m，n，p，q∈N*)若k＋l＝m＋n(k，l，m，n∈N*)，则ak·al＝am·an•课时小结•布置作业1.课代表抽查默写公式2.完成学考材料P33-34