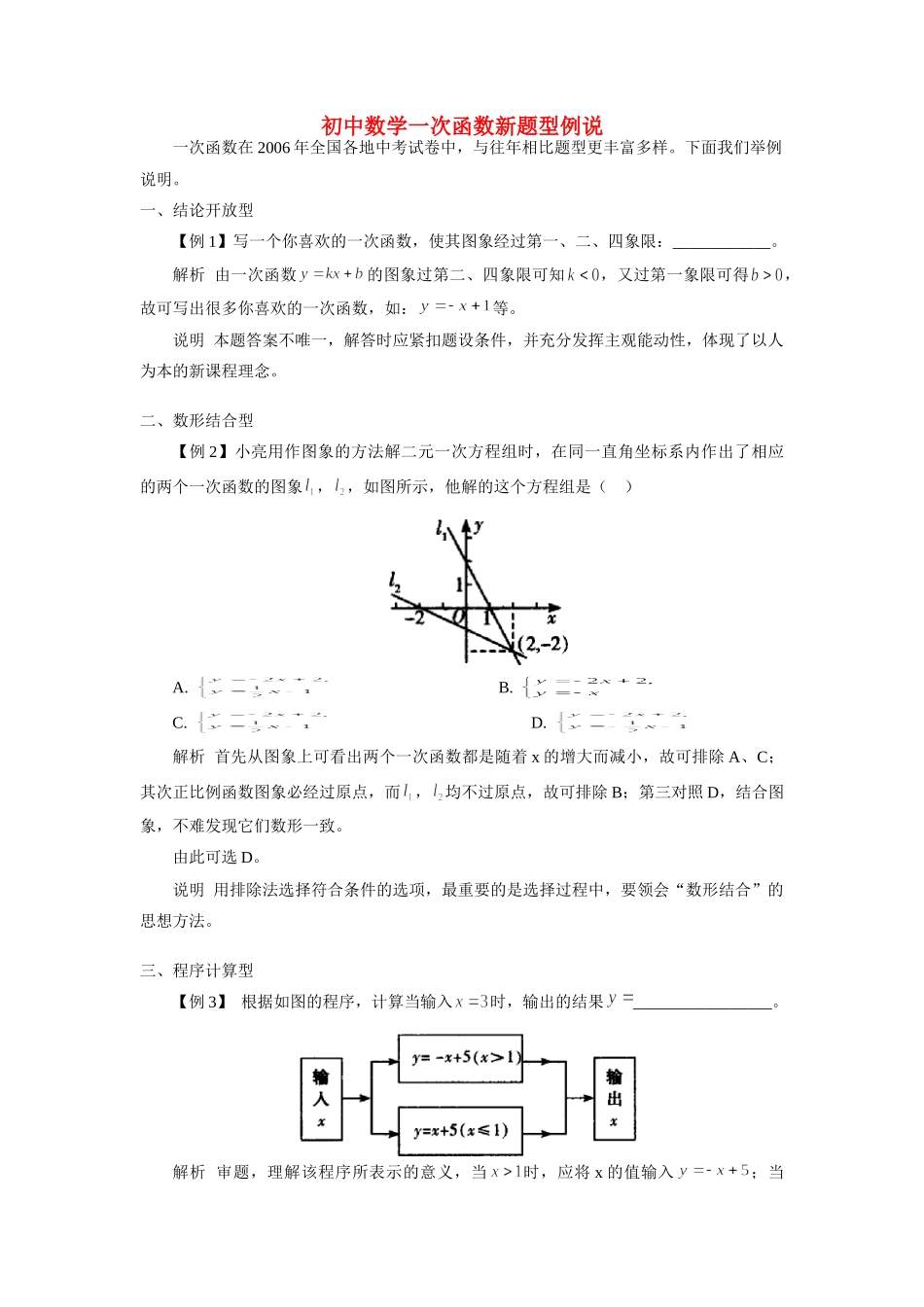
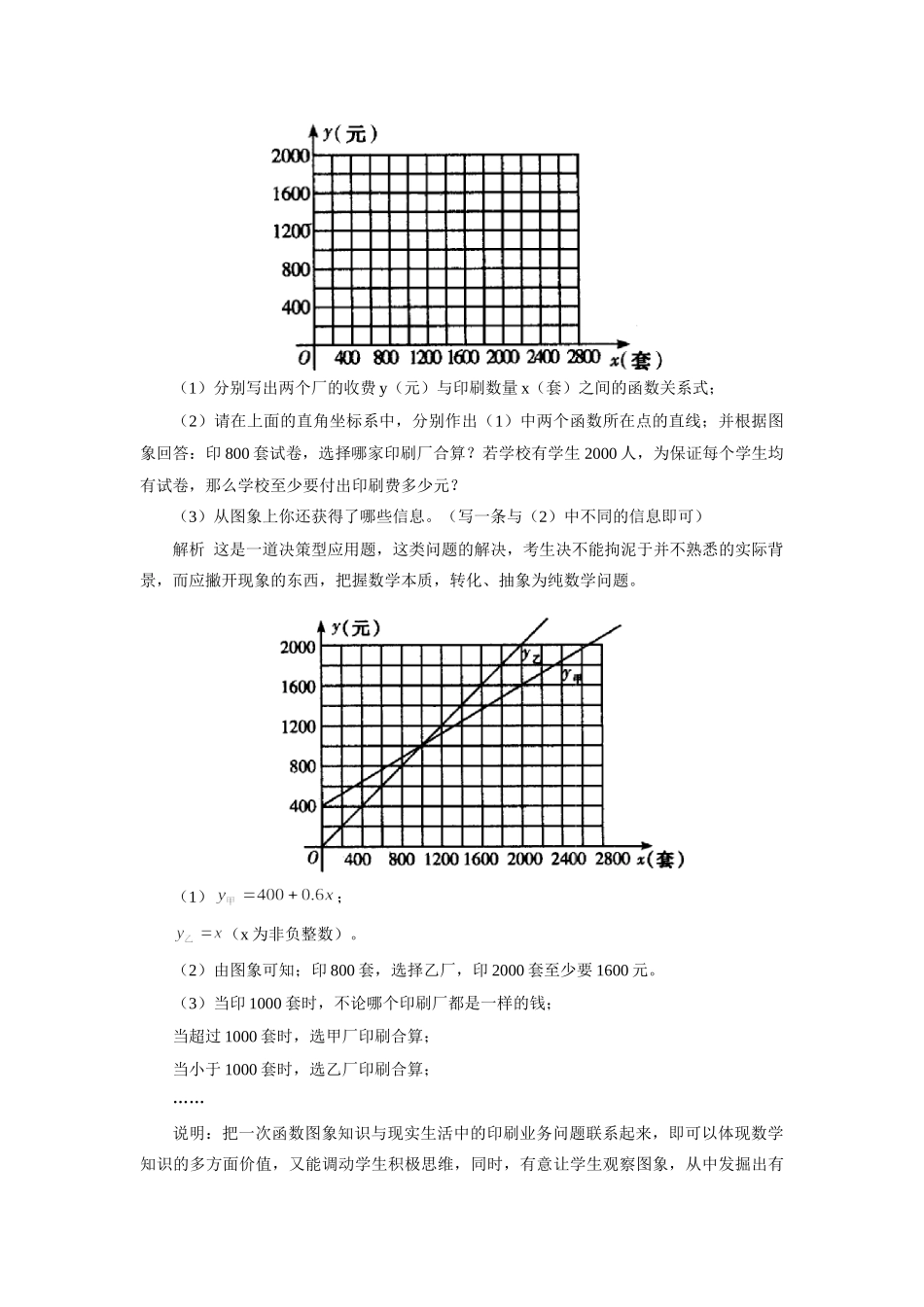
初中数学一次函数新题型例说一次函数在2006年全国各地中考试卷中,与往年相比题型更丰富多样。下面我们举例说明。一、结论开放型【例1】写一个你喜欢的一次函数,使其图象经过第一、二、四象限:____________。解析由一次函数的图象过第二、四象限可知,又过第一象限可得,故可写出很多你喜欢的一次函数,如:等。说明本题答案不唯一,解答时应紧扣题设条件,并充分发挥主观能动性,体现了以人为本的新课程理念。二、数形结合型【例2】小亮用作图象的方法解二元一次方程组时,在同一直角坐标系内作出了相应的两个一次函数的图象,,如图所示,他解的这个方程组是()A.B.C.D.解析首先从图象上可看出两个一次函数都是随着x的增大而减小,故可排除A、C;其次正比例函数图象必经过原点,而,均不过原点,故可排除B;第三对照D,结合图象,不难发现它们数形一致。由此可选D。说明用排除法选择符合条件的选项,最重要的是选择过程中,要领会“数形结合”的思想方法。三、程序计算型【例3】根据如图的程序,计算当输入时,输出的结果_________________。解析审题,理解该程序所表示的意义,当时,应将x的值输入;当时,则将x的值输入,故当时,=2。说明本题渗透了计算机程序设计,同时考查了学生阅读理解能力。四、平移图象型【例4】直线向右平移3个单位,再向下平移2个单位,所得到的直线的解析式是_________________。解析一:如下图所示,依次画出直线平移的图象,注意左右平移应沿x轴,上下平移应沿y轴。解析二:在直线上任取两点A(0,2),B(1,3)。由题意知:点A向右平移3个单位,再向下平移2个单位后得A′(3,0);点B(1,3)向右平移3个单位,再向下平移2个单位后得B′(4,1)。设平移后的直线的解析式A′B′为,则点A′(3,0),B′(4,1)在该直线上,所以解得。故平移后的直线A′B′的解析式为。说明解析一是应用图象法,直观明了;解析二采用特殊值法和待定系数法,有章可循。两者结合,相得益彰。五、决策应用型【例5】某中学要印制期末考试卷,甲印刷厂提出:每套试卷收0.6元印刷费,另收400元制版费;乙印刷厂提出:每套试卷收1元印刷费,不再收取制版费。(1)分别写出两个厂的收费y(元)与印刷数量x(套)之间的函数关系式;(2)请在上面的直角坐标系中,分别作出(1)中两个函数所在点的直线;并根据图象回答:印800套试卷,选择哪家印刷厂合算?若学校有学生2000人,为保证每个学生均有试卷,那么学校至少要付出印刷费多少元?(3)从图象上你还获得了哪些信息。(写一条与(2)中不同的信息即可)解析这是一道决策型应用题,这类问题的解决,考生决不能拘泥于并不熟悉的实际背景,而应撇开现象的东西,把握数学本质,转化、抽象为纯数学问题。(1);(x为非负整数)。(2)由图象可知;印800套,选择乙厂,印2000套至少要1600元。(3)当印1000套时,不论哪个印刷厂都是一样的钱;当超过1000套时,选甲厂印刷合算;当小于1000套时,选乙厂印刷合算;……说明:把一次函数图象知识与现实生活中的印刷业务问题联系起来,即可以体现数学知识的多方面价值,又能调动学生积极思维,同时,有意让学生观察图象,从中发掘出有用的信息,也显得非常必要。