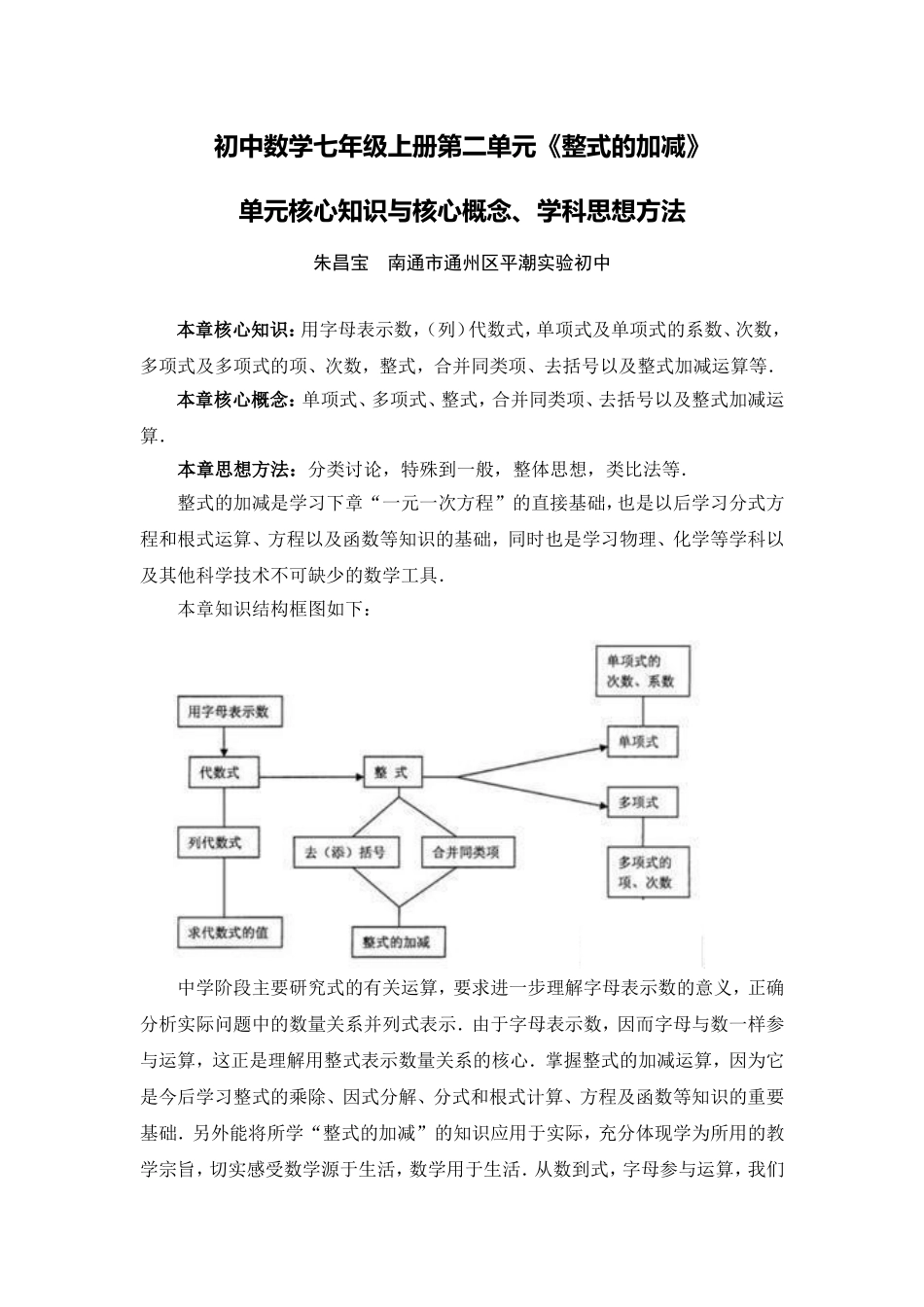
初中数学七年级上册第二单元《整式的加减》单元核心知识与核心概念、学科思想方法朱昌宝南通市通州区平潮实验初中本章核心知识:用字母表示数,(列)代数式,单项式及单项式的系数、次数,多项式及多项式的项、次数,整式,合并同类项、去括号以及整式加减运算等.本章核心概念:单项式、多项式、整式,合并同类项、去括号以及整式加减运算.本章思想方法:分类讨论,特殊到一般,整体思想,类比法等.整式的加减是学习下章“一元一次方程”的直接基础,也是以后学习分式方程和根式运算、方程以及函数等知识的基础,同时也是学习物理、化学等学科以及其他科学技术不可缺少的数学工具.本章知识结构框图如下:中学阶段主要研究式的有关运算,要求进一步理解字母表示数的意义,正确分析实际问题中的数量关系并列式表示.由于字母表示数,因而字母与数一样参与运算,这正是理解用整式表示数量关系的核心.掌握整式的加减运算,因为它是今后学习整式的乘除、因式分解、分式和根式计算、方程及函数等知识的重要基础.另外能将所学“整式的加减”的知识应用于实际,充分体现学为所用的教学宗旨,切实感受数学源于生活,数学用于生活.从数到式,字母参与运算,我们可以得到形式各一的式子.掌握合并同类项的运算法则,灵活应用合并同类项法则进行整式加减运算,并会进行相关的化简求值.在具体实施概念教学时,我们可以通过以下几个过程来实施:(1)概括.数学概念的获得有两种基本形式:一种是顺应.即从大量具体例子出发,从学生实际经验的肯定例证中,以归纳的方法概括出一类事物的本质属性,这种获得概念的方式称为概念形成.另一种是向学生展示定义,利用原有认知结构中的有关知识理解新概念,这种方式称为概念同化.可以说概念形成主要依赖的是对具体事物的抽象概括,而概念同化主要依赖的是学生对经验的概括和新旧知识的联系.(2)表述.对某类具有相同关键特征的事物进行命名,根据实际选择一种易于学生理解的方式揭示概念的本质,陈述定义.(3)识别.在给出概念表述以后,教师应该区分学生对新概念是否真正理解了.为此,可以举出一些该概念外延之内或之外的例子,让学生根据定义进行判别练习,通过这样的练习可以帮助学生更加准确地把握概念的本质特征,排除无关特征,从而真正理解概念.可通过快速抢答、智力大比拼等途径,为学生强化概念,深刻理解概念的内涵与外延创设了较大的探索空间.(4)运用.对已经获得的概念在知觉水平和思维水平上进行运用.所谓在知觉水平上运用就是指当遇到这类事物的特征时,能立即把他看作是一类事物的具体例子;而在思维水平上进行运用则指新的概念或命题已经属于包括水平较高的原有概念或命题中,或一类已知事物的一个新的不太明显的代表被识别出来.对数学概念的学习不仅要注意知觉水平上的运用,还要注意在思维水平上的运用.在核心概念的讲解中,教师的有效引导让学生的思维在交流中、摩擦中、碰撞中得到有效滋养,正所谓的是根深方可叶茂.由具体的数到用字母表示数,可以简明地表达一些一般数量和数量关系,给研究问题和计算带来方便.教科书中选择学生熟悉的数量关系的实际问题,主要目的就是让学生经历分析实际问题中的数量关系,体会核心概念及整式的运算来源于实际,感受从特殊到一般的数学方法,学会由实际问题抽象出数学问题的过程,体会整式比数字更具一般性的道理,初步接触建模思想.从具体数的计算到用式子表示数量关系也是一个由特殊到一般的过程;在整式的化简求值过程中,则是由一般到特殊的过程,这样的安排可以让学生学会辩证的思考问题,从不同的视野获取新知.在整式的计算过程中,由于每个字母都表示数,因此学生可以通过类比思想,探索整式的一些运算规律.例如利用分配律可以合并同类项、去括号,从而进行整式的加减运算.