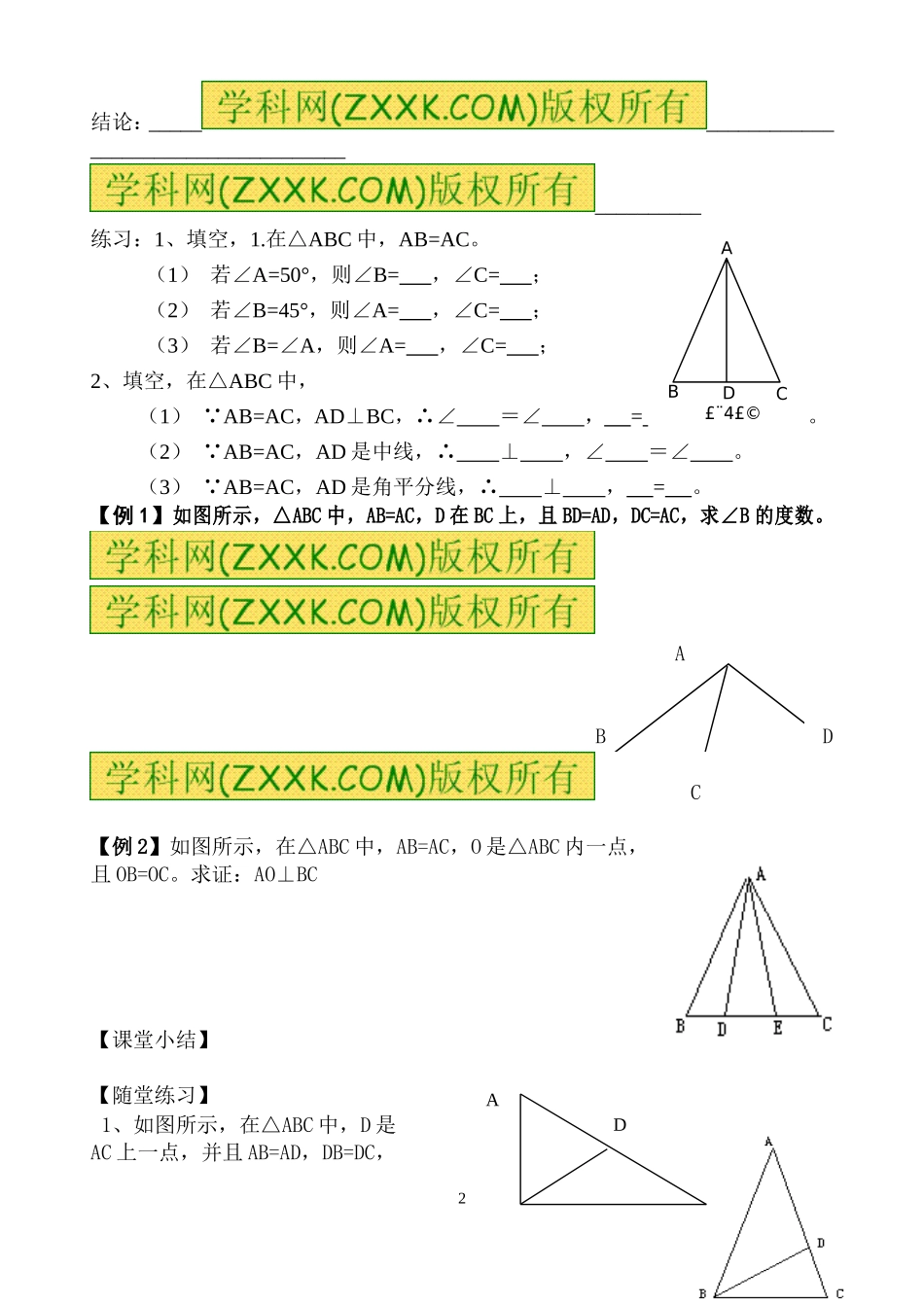
1市三十三中导学稿★八年级数学下★第1期课题:第一章第1节等腰三角形(第1课时)主备:魏秋梅审批:唐明举审核:王勇班级:学生姓名:【学习目标】知识与技能:能证明等腰三角形的性质。过程与方法:经历“探索--发现--猜想--证明”的过程,逐步掌握综合法证明的方法。情感与态度:发展学生的推理能力。【教学重点、难点】重点:能证明等腰三角形的性质。难点:证明过程的推导书写。【学前准备】1、什么叫公理?什么叫定理?2、列举我们已知道的公理:(1)公理:同位角,两直线平行。(2)公理:两直线,同位角。(3)公理:的两个三角形全等。(4)公理:的两个三角形全等。[来源:学科网ZXXK](5)公理:的两个三角形全等。(6)公理:全等三角形的对应边,对应角。注:等式的有关性质和不等式的有关性质都可以看作公理。【自学探究】利用已有的公理和定理证明:“两角及其中一角的对边对应相等的两个三角形全等。”【师生探究,合作交流】定理:等腰三角形的两底角相等。简述为:等边对等角。在上题中,线段AD还具有怎样的性质?为什么?你能得到什么结论?2结论:___________________________________________________练习:1、填空,1.在△ABC中,AB=AC。(1)若∠A=50°,则∠B=,∠C=;(2)若∠B=45°,则∠A=,∠C=;(3)若∠B=∠A,则∠A=,∠C=;2、填空,在△ABC中,(1) AB=AC,AD⊥BC,∴∠=∠,=。(2) AB=AC,AD是中线,∴⊥,∠=∠。(3) AB=AC,AD是角平分线,∴⊥,=。【例1】如图所示,△ABC中,AB=AC,D在BC上,且BD=AD,DC=AC,求∠B的度数。ABDC【例2】如图所示,在△ABC中,AB=AC,O是△ABC内一点,且OB=OC。求证:AO⊥BC【课堂小结】【随堂练习】1、如图所示,在△ABC中,D是AC上一点,并且AB=AD,DB=DC,ABCD£¨4£©DA3若∠C=290,则∠A=________2、如图在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数?【当堂检测】1、下列各组几何图形中,一定全等的是()A、各有一个角是550的两个等腰三角形;B、两个等边三角形;C、腰长相等的两个等腰直角三角形;D、各有一个角是500,腰长都为6cm的两个等腰三角形.2、如图,已知:∥,AB=CD,若要使△ABE≌△CDF,仍需添加一个条件,下列条件中,哪一个不能使△ABE≌△CDF的是()A、∠A=∠DB、BF=CE;C、AE∥DFD、AE=DF3、如果等腰三角形的一个内角等于500则其余两角的度数为。4、如果等腰三角形的一条边长为3,另一边长为5,则它的周长为。如果等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的腰长为。5、△ABC中,AB=AC,且BD=BC=AD,则∠A的度数为。【今日作业】习题1.11,2,3BC4【中考链接】已知:如图,△ABC中,AD是高,CE是中线,DC=BE,DG⊥CE,G是垂足,求证:(1)G是CE中点(2)∠B=2∠BCE[来源:学科网]市三十三中导学稿★八年级数学下★第2期课题:第一章第1节等腰三角形(第2课时)主备:魏秋梅审批:唐明举审核:王勇班级:学生姓名:【学习目标】知识与技能:能证明等腰三角形的性质。掌握“等边三角形判定”,会用其进行相关的计算和证明。过程与方法:经历“探索--发现--猜想--证明”的过程,逐步掌握综合法证明的方法。情感与态度:发展学生的推理能力。【教学重点、难点】重点:能证明等腰三角形的性质,等边三角形的判定。难点:证明过程的推导书写。【学前准备】1、等腰三角形的性质是什么?[来源:学科网]2、等腰三角形的一个内角为700,则顶角为。3、等腰三角形的一个外角为1000,则其顶角为。【自学探究】1、等腰三角形的两底的角平分线相等吗?怎样证明。已知:求证:证明:5[来源:Z&xx&k.Com]得出定理:。问题:等腰三角形两条腰上的中线相等吗?高呢?还有其他的结论吗?请你证明它们,并与同伴交流。【师生探究,合作交流】1、等边三角形是特殊的等腰三角形,除具有等腰三角形的性质外,还有特殊的性质吗?已知:求证:[来源:学科网ZXXK]证明:得出定理:。练习:1.已知,如右图,等腰△ABC,AB=AC:(1)若AB=BC,则△ABC为__________三角形;(2)若∠A=60°,则△ABC为__________三角形;(3)若∠B=60°,则△ABC为__________三角形.2.在线段、直角...