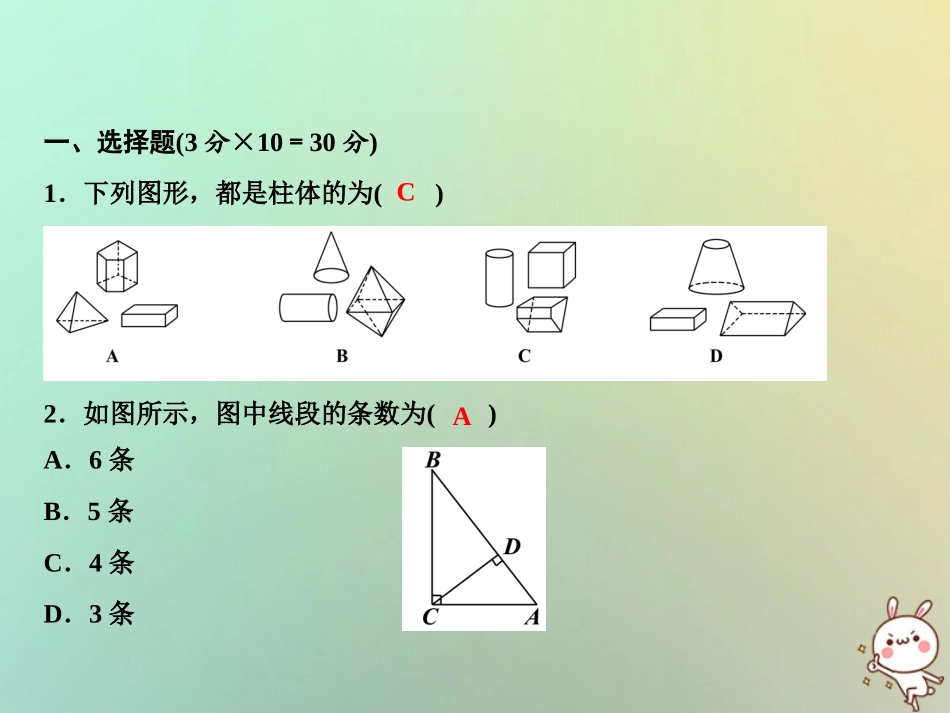
第4章综合检测题(检测时间:120分钟满分:120分)2018年秋数学七年级上册•HS一、选择题(3分×10=30分)1.下列图形,都是柱体的为()2.如图所示,图中线段的条数为()A.6条B.5条C.4条D.3条CA3.下列几何体中,同一个几何体的主视图与俯视图不同的是()4.下面四个图形每个都是由六个相同的正方形组成,将其折叠后能围成正方体的是()CC5.下列说法:①延长直线AB;②延长线段AB;③延长射线AB;④画直线AB=3cm;⑤在射线AB上截取线段AC,使AC=3cm.其中正确的有()A.1个B.2个C.3个D.4个6.如图,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是()A.20°B.25°C.30°D.70°BD7.下列四种说法:①因为AM=MB,所以M是AB的中点;②在线段AM的延长线上取一点B,如果AB=2AM,那么M是AB的中点;③因为M是AB的中点,所以AM=MB=12AB;④因为A、M、B在同一条直线上,且AM=BM,所以M是AB的中点.其中正确的是()A.①③④B.④C.②③④D.③④C8.如图,甲从点A出发向北偏东70°方向走50m至点B,乙从点A出发向南偏西15°方向走80m到点C,则∠BAC的度数是()A.85°B.160°C.125°D.105°9.一个锐角的补角与这个锐角的余角的差是一个()A.锐角B.直角C.钝角D.锐角或直角或钝角CB10.中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池.类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,则该几何体为()A二、填空题(3分×8=24分)11.如图,图中共有条线段,个角.12.一个角的补角是36°35′,这个角是.13.下列现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设;④把弯曲的公路改直,就能缩短路程.其中可用“两点确定一条直线”来解释的现象有.14.把15°30′化成度的形式,则15°30′=度.1012143°25′①②15.515.如图,D是AC的中点,且BC=13AC,DC=3cm,则AB=cm.16.如图,∠AOD=130°,∠COD=60°,OB是∠AOC的平分线,则∠AOB=.17.如图是由五块小立方体堆成的一个几何体,则从上面看有个正方形,从正面看有个正方形,从左面看有个正方形.18.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为.435°35324三、解答题(共66分)19.(10分)计算:(1)36°55′+32°15′;(2)90°÷7(精确到1″).解:(1)69°10′;(2)12°51′26″.20.(10分)5个棱长为1的正方体组成如图的几何体.(1)该几何体的体积是(立方单位),表面积是(平方单位);(2)画出该几何体的主视图(从正面看)和左视图(从左面看).522解:画图略.21.(8分)已知∠1和∠2互为补角,∠2的度数的一半比∠1大45°,试求出∠1与∠2的度数.解:∠1=30°,∠2=150°.22.(8分)如图,OB平分∠COD,∠AOB=90°,∠AOC=125°.求∠COD的度数.解:70°.23.(10分)如图,某轮船上午8时在A处,测得灯塔S在北偏东60°的方向上,向东行驶至中午12时,轮船到达B处,在B处测得灯塔S在北偏西30°的方向上,已知轮船行驶速度为20千米/时.(1)在图中画出灯塔S的位置;(2)量一量,算一算,求出船在B处时,离灯塔S的实际距离.解:(1)作图略;(2)约为40km.24.(8分)如图,C是AB的中点,D、E分别是线段AC、CB上的点,且AD=23AC,DE=35AB.若AB=24cm,求线段CE的长.解:∵AC=12AB,AD=23AC,∴AD=13AB,∴BE=AB-AD-DE=AB-13AB-35AB=115AB,∴CE=AB-AC-BE=1330AB=10.4(cm).25.(12分)(1)如图①,已知∠AOB=80°,OC是∠AOB的平分线,OD平分∠BOC,OE平分∠AOC.求∠DOE的度数;(2)如图②,在(1)中,把“OC是∠AOB的平分线”改为“OC为∠AOB内任意一射线”,其他条件不变.试求∠DOE的度数;(3)如图③,在(1)中,把“OC是∠AOB的平分线”改为“OC是∠AOB外的一条射线”,其他条件都不变.能否求出∠DOE的度数,说明理由;(4)在(3)中,若把“∠AOB=80°”改为“∠AOB=α”,其他不变.则∠DOE为多少度?从中你能得出什么规律.解:(1)40°;(2)40°;(3)能.理由:由题可知,∠BOD=∠COD=12∠BOC,∠AOE=∠COE=12∠AOC,又∵∠DOE=∠DOC-∠COE,∴∠DOE=∠BOD-∠AOE=∠AOB-AOD-∠AOE=∠AOB-∠DOE,即∠DOE=12∠AOB,∵∠AOB=80°,∴∠DOE=40°;(4)∠DOE=α2.