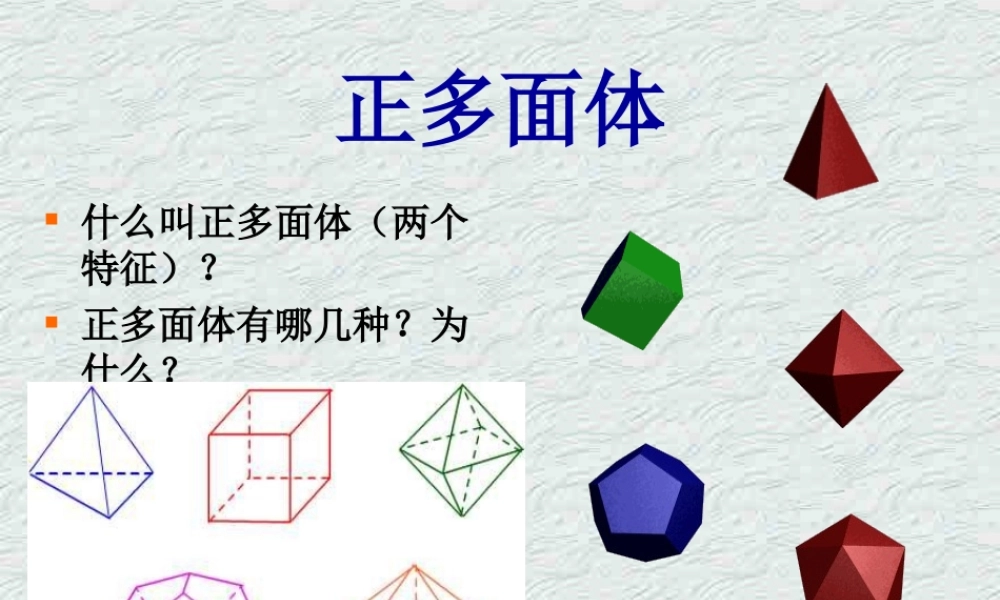
正多面体 什么叫正多面体(两个特征)? 正多面体有哪几种?为什么?问题 1. 图中有 5 个多面体 , 分别数出它们的顶点数 V, 面数 F 和棱数 E, 并填表 :12345图形编号顶点数 V面数 F棱数 E123454468612681298159916规律 :V+F-E=2问题 2. 图中有三个多面体,分别数出它们的顶点数 V 、面数 F 和棱数 E,并填表。 13图形编号顶点数 V面数 F棱数 E1 235 5 8这些图形符合前面找出的规律V+F-E=2 吗 ?12 12 247 8 122比较问题 1 和问题 2 中的图形,如果这些多面体的表面都是用橡皮薄膜制作的,并且可以向它们的内部充气那么其中哪些多面体能够连续(不破裂)变形,最后其表面可变为一个球面? 像以上那样的连续变形中,表面能变为一个球面的多面体 , 叫简单多面体 . 想一想 前面的多面体中,是简单多面体的有哪些?棱柱、棱锥、正多面体、凸多面体是简单多面体吗?猜想 简单多面体的顶点数 V ,面数 F 的和与棱数 E 之间存在的规律? V+F-E=2 欧拉,瑞士数学家。 13 岁就成为巴塞尔大学的学生, 17 岁成为巴塞尔有史以来的第一个年轻的硕士。欧拉从一开始就选择通过解决实际问题进行数学研究的道路。 1726 年, 19 岁的欧拉由于撰写了《论桅杆配置的船舶问题》而荣获巴黎科学院的资金。 欧拉的成才还有另一个重要的因素,就是他那惊人的记忆力!他能背诵前一百个质数的前十次幂,能背诵罗马诗人维吉尔( Virgil )的史诗 Aeneil ,能背诵全部的数学公式。直至晚年,他还能复述年轻时的笔记的全部内容。高等数学的计算他可以用心算来完成。 欧拉最先把对数定义为乘方的逆运算,并且最先发现了对数是无穷多值的。他证明了任一非零实数R有无穷多个对数。 欧拉使三角学成为一门系统的科学,他首先用比值来给出三角函数的定义,使三角学跳出只研究三角表这个圈子。欧拉对整个三角学作了分析性的研究,从最初几个公式解析地推导出了全部三角公式,还获得了许多新的公式。 欧拉用 a 、 b 、 c 表示三角形的三条边,用A、B、C表示第个边所对的角,从而使叙述大大地简化。欧拉得到的著名的公式又把三角函数与指数函联结起来。 在普及教育和科研中,欧拉意识到符号的简化和规则化既有有助于学生的学习,又有助于数学的发展,所以欧拉创立了许多新的符号。如用 sin 、cos 等表示三角函数,用 e 表示自然对数的底,用 f(x) 表示函数,用 ∑表示求...