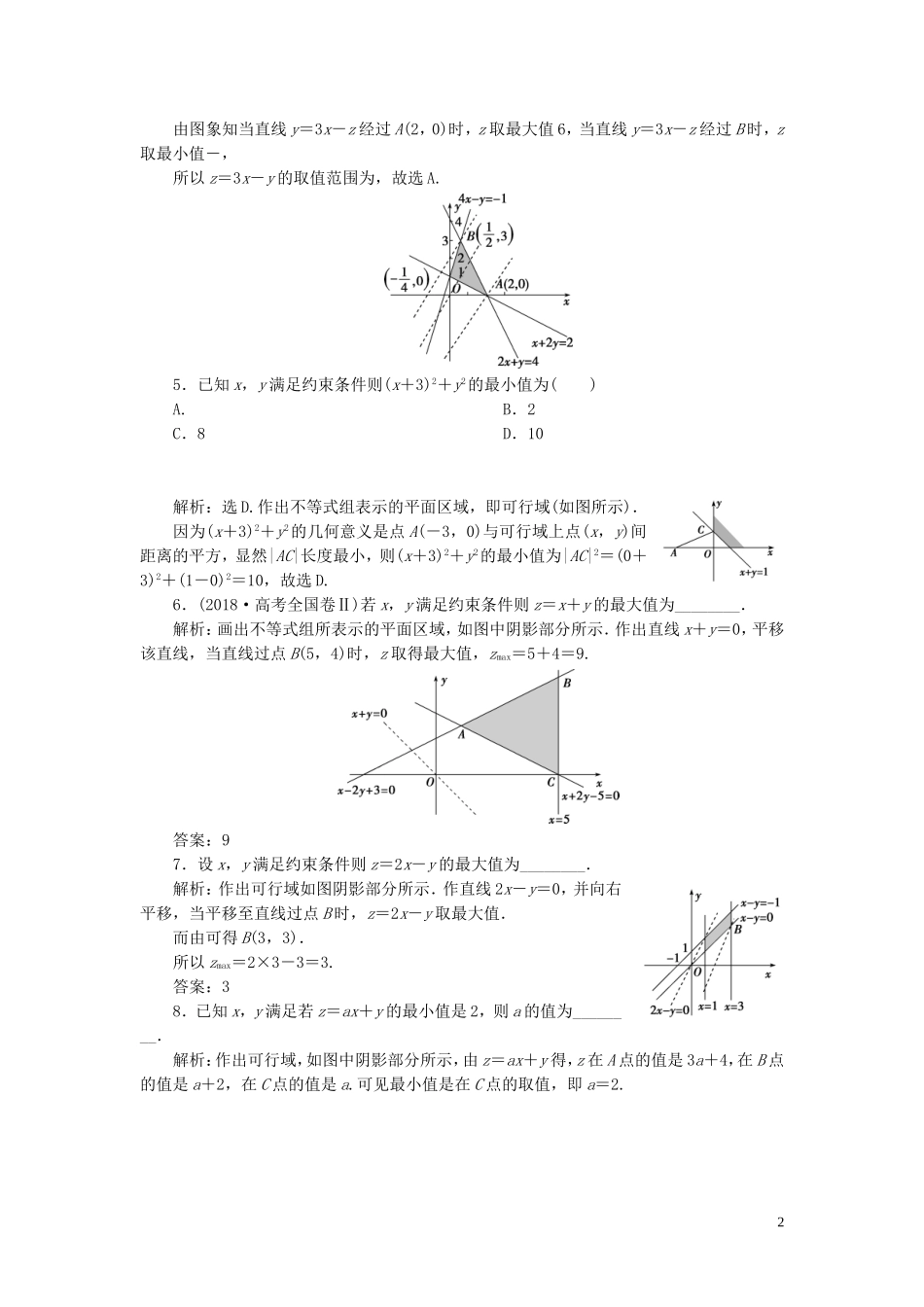
第 1 课时 简单的线性规划问题 [A 基础达标]1.若变量 x,y 满足约束条件则 2x+y 的最大值是( )A.2 B.4C.7 D.8解析:选 C.画出可行域如图(阴影部分).设目标函数为 z=2x+y,由解得 A(3,1),当目标函数过 A(3,1)时取得最大值,所以 zmax=2×3+1=7,故选 C.2.若变量 x,y 满足约束条件则 z=x-2y 的最大值为( )A.4 B.3C.2 D.1解析:选 B.画出可行域(如图),由 z=x-2y,得 y=x-,则当目标函数过 C(1,-1)时取得最大值,所以 zmax=1-2×(-1)=3.3.已知 x,y 满足约束条件则 z=-2x+y 的最大值是( )A.-1 B.-2C.-5 D.1解析:选 A.作出可行域,如图所示,当 z=-2x+y 经过点 A 时,z 取得最大值,由得 A(1,1),则 zmax=-2×1+1=-1.4.设变量 x,y 满足约束条件则目标函数 z=3x-y 的取值范围是( )A. B.C.[-1,6] D.解析:选 A.约束条件所表示的平面区域如图阴影部分,直线 y=3x-z 的斜率为 3.1由图象知当直线 y=3x-z 经过 A(2,0)时,z 取最大值 6,当直线 y=3x-z 经过 B 时,z取最小值-,所以 z=3x-y 的取值范围为,故选 A.5.已知 x,y 满足约束条件则(x+3)2+y2的最小值为( )A. B.2C.8 D.10解析:选 D.作出不等式组表示的平面区域,即可行域(如图所示).因为(x+3)2+y2的几何意义是点 A(-3,0)与可行域上点(x,y)间距离的平方,显然|AC|长度最小,则(x+3)2+y2的最小值为|AC|2=(0+3)2+(1-0)2=10,故选 D.6.(2018·高考全国卷Ⅱ)若 x,y 满足约束条件则 z=x+y 的最大值为________.解析:画出不等式组所表示的平面区域,如图中阴影部分所示.作出直线 x+y=0,平移该直线,当直线过点 B(5,4)时,z 取得最大值,zmax=5+4=9.答案:97.设 x,y 满足约束条件则 z=2x-y 的最大值为________.解析:作出可行域如图阴影部分所示.作直线 2x-y=0,并向右平移,当平移至直线过点 B 时,z=2x-y 取最大值.而由可得 B(3,3).所以 zmax=2×3-3=3.答案:38.已知 x,y 满足若 z=ax+y 的最小值是 2,则 a 的值为________.解析:作出可行域,如图中阴影部分所示,由 z=ax+y 得,z 在 A 点的值是 3a+4,在 B 点的值是 a+2,在 C 点的值是 a.可见最小值是在 C 点的取值,即 a=2.2答案:29.设 z=2y-2x+5,其中 x,y 满足约束条件求 z 的...