典型例题(同名13005)VIP免费

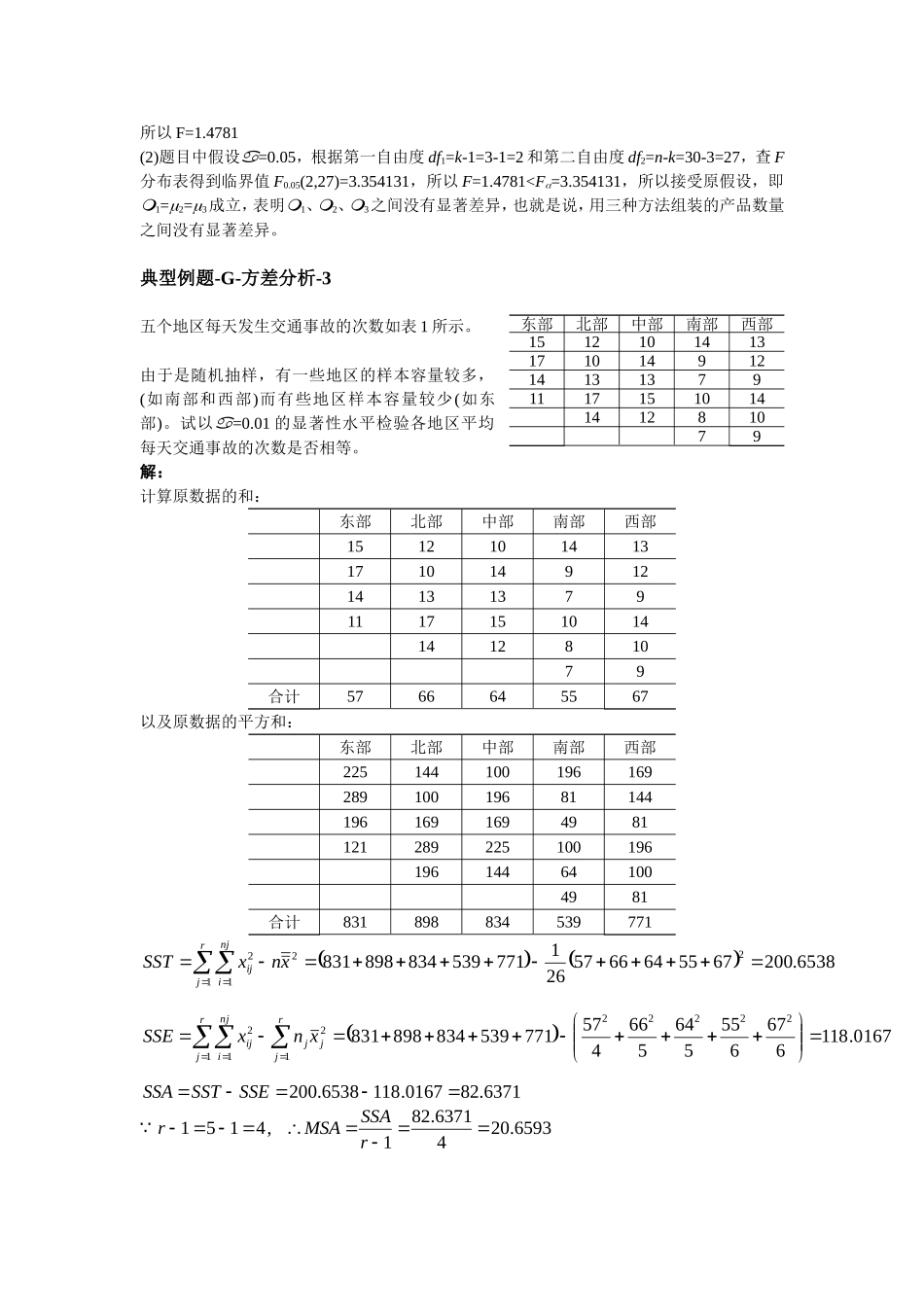
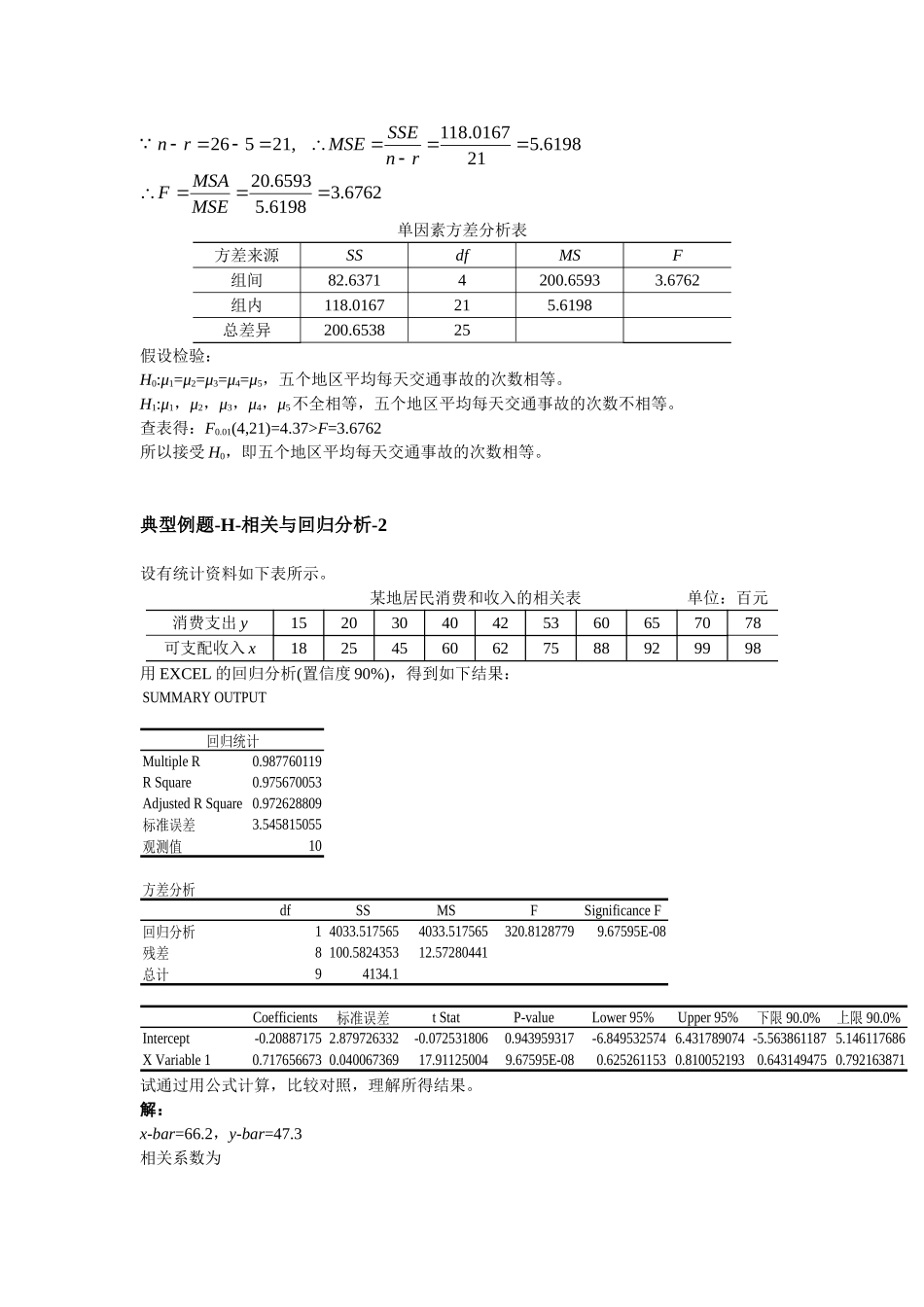
典型例题-G-方差分析-2某企业准备用三种方法组装一种新的产品，为确定哪种方法每小时生产的产品数量最多，随机抽取了30名工人，并指定每个人使用其中的一种方法。通过对每个工人生产的产品数进行方差分析，得到如下表所示的结果。每个工人生产产品数量的方差分析表差异源SSdfMSFP-valueFcrit组间③①210⑥0.2459463.354131组内3836②⑤———总计④29————(1)完成上面的方差分析表(2)若显著性水平为=0.05，检验三种方法组装的产品数量之间是否有显著差异。解：(1)完成方差分析表，以表格中所标的①、②、③、④、⑤、⑥为顺序，来完成表格，具体步骤如下：①求k-1根据题目中“该企业准备用三种方法组装一种新的产品”可知，因素水平(总体)的个数k=3，所以第一自由度df1=k-1=3-1=2，即SSA的自由度。②求n-k由“随机抽取了30名工人”可知，全部观测值的个数n=30，因此可以推出第二自由度df2=n-k=30-3=27，即SSE的自由度。③求组间平方和SSA已知第一自由度df1=k-1=3-1=2，MSA=210根据公式1kSSAMSA自由度组间平方和所以，SSA=MSA×(k-1)=210×2=420④求总误差平方和SST由上面③中可以知道SSA=420；此外从表格中可以知道：组内平方和SSE=3836，根据公式SST=SSA+SSE可以得出SST=420+3836=4256，即总误差平方和SST=4256⑤求SSE的均方MSE已知组内平方和SSE=3836，SSE的自由度n-k=30-3=27根据公式0741.142273836knSSEMSE自由度组内平方和所以组内均方MSE=142.0741⑥求检验统计量F已知MSA=210，MSE=142.0741根据4781.10741.142210MSEMSAF所以F=1.4781(2)题目中假设=0.05，根据第一自由度df1=k-1=3-1=2和第二自由度df2=n-k=30-3=27，查F分布表得到临界值F0.05(2,27)=3.354131，所以F=1.4781F=3.6762所以接受H0，即五个地区平均每天交通事故的次数相等。典型例题-H-相关与回归分析-2设有统计资料如下表所示。某地居民消费和收入的相关表单位：百元消费支出y15203040425360657078可支配收入x18254560627588929998用EXCEL的回归分析(置信度90%)，得到如下结果：SUMMARYOUTPUT回归统计MultipleR0.987760119RSquare0.975670053AdjustedRSquare0.972628809标准误差3.545815055观测值10方差分析dfSSMSFSignificanceF回归分析14033.5175654033.517565320.81287799.67595E-08残差8100.582435312.57280441总计94134.1Coefficients标准误差tStatP-valueLower95%Upper95%下限90.0%上限90.0%Intercept-0.208871752.879726332-0.0725318060.943959317-6.8495325746.431789...