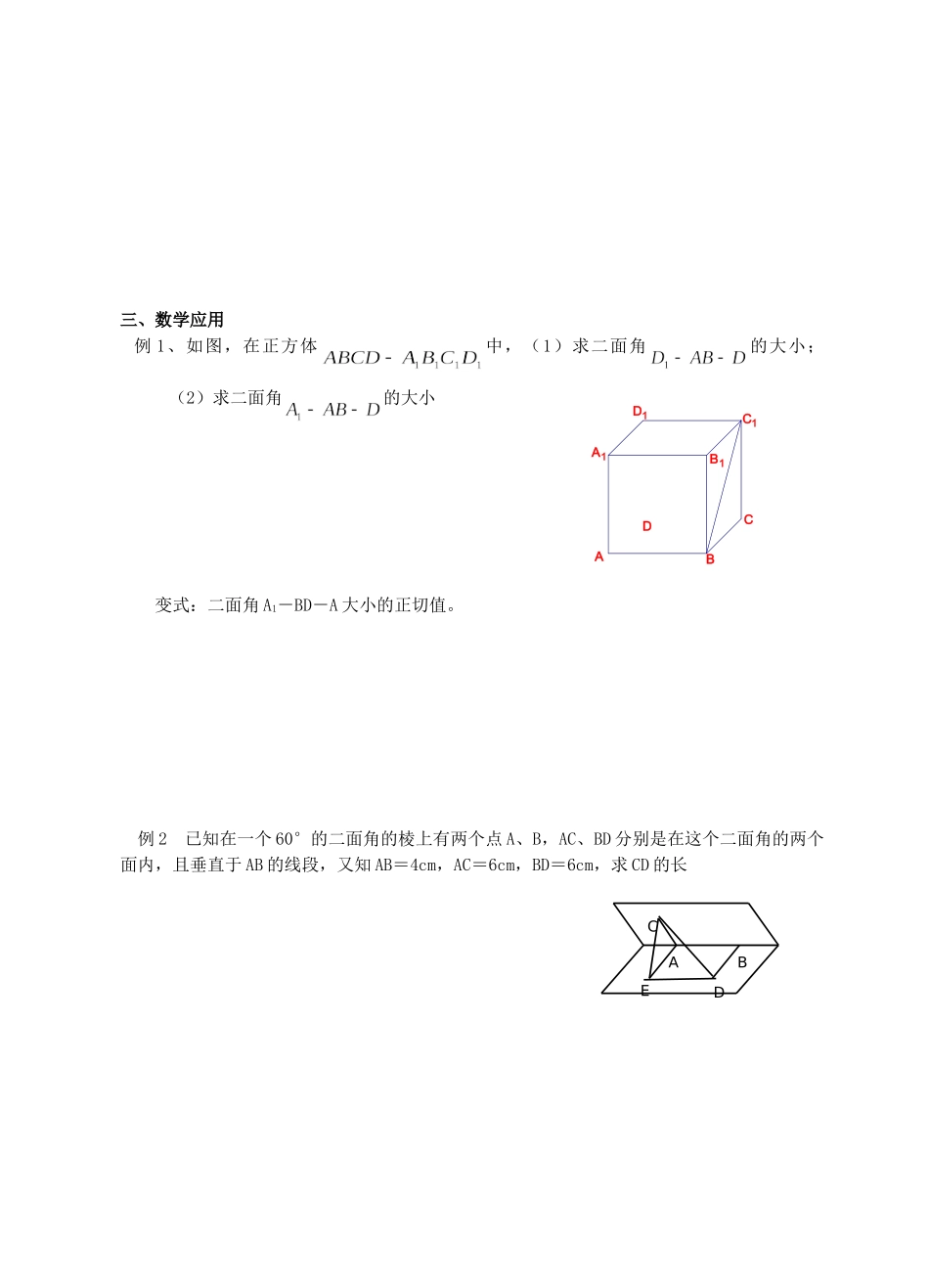
必修必修 2 2 第一章 空间立体几何课题:§1.2.3 平面与平面的位置关系(2) 总第 30 个课时教学目标:1、使学生正确理解和掌握二面角、二面角的平面角的概念,会用不同的方法作出二面角平面角;并能掌握其初步应用;2、引导学生探索、研究“二面角的平面角”应该如何定义,在概念的形成过程3、发展学生的思维能力,培养学生类比、观察、归纳总结的能力;通过创设问题情境,联系生活的实际,培养学生学习数学的兴趣,明白数学和生活紧密相连;通过共同讨论、解决问题,培养学生交流与合作的协作精神。教学重点:求二面角平面角的几种常用方法教学难点:找二面角的平面角教学过程:一、问题情境回忆什么是角?如何表示?如何刻画两个平面形成的这种“角”呢?二、学生活动 问题 1.你能否从刚才的图片中抽象出一定的数学模型? 问题 2.请同学们拿出一张纸,你能否用这张纸制作这个模型吗? 问题 3.当我们把这张纸沿着其中的一条直线折叠就得到刻画空间两个相交平面形成的一种“角”,对于这种如何定义?三、建构数学1、半平面: 2、二面角、棱、面:问题 5.你能把你制作的模型用图形表示在平面上吗?二面角的画法:平卧式 直立式 问题 6.当纸板沿着折痕不断打开的时候,我们感到两个面构成的二面角在逐渐变大,如何来刻画这个二面角的大小?3、二面角的平面角:一般地,以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角4、平面角的范围:问题 7.二面角的大小与点 O 的位置有关吗?平面角必须满足哪几个条件?lll三、数学应用例 1、如图,在正方体中,(1)求二面角的大小;(2)求二面角的大小 变式:二面角 A1-BD-A 大小的正切值。例 2 已知在一个 60°的二面角的棱上有两个点 A、B,AC、BD 分别是在这个二面角的两个面内,且垂直于 AB 的线段,又知 AB=4cm,AC=6cm,BD=6cm,求 CD 的长D1C1B1A1DCBAABCDE变式:如图二面角 α-l-β 中,CA⊥l 于 A,BD⊥l 于 B,又知 AB=4cm,AC=6cm,BD=6cm,CD= ,求二面角 α-l-β 的大小。四、当堂反馈1、书P1、32、二面角是指 ( )A.两个平面相交所组成的图形 B.一个平面绕这个平面内一条直线旋转所组成的图形 C.从一个平面内的一条直线出发的一个半平面与这个平面所组成的图形 D.从一条直线出发的两个半平面所组成的图形3、如图,射线、、两两互相垂直,,,则弧...