黑体辐射定律

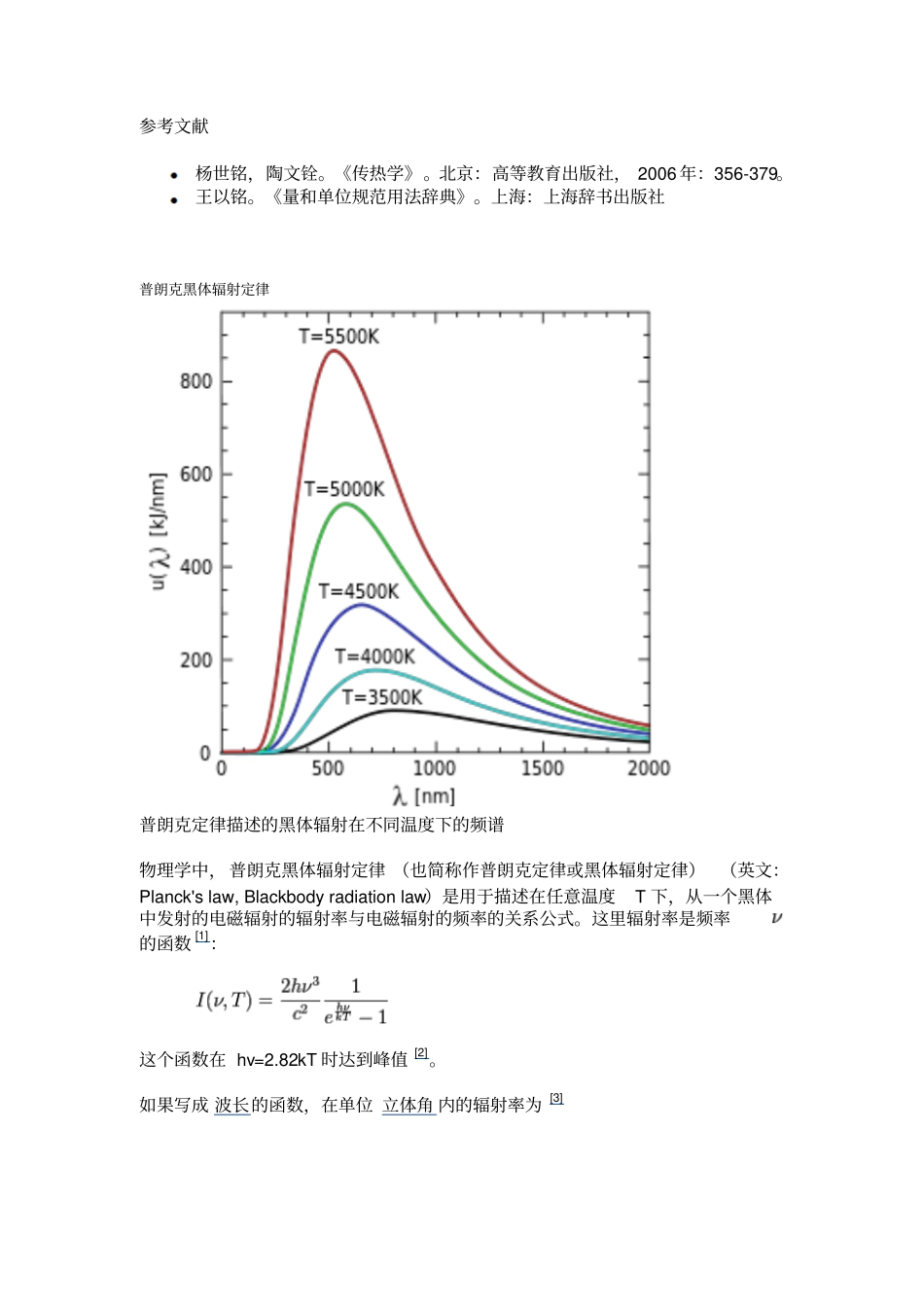
基尔霍夫热辐射定律基尔霍夫热辐射定律（ Kirchhoff 热辐射定律），德国物理学家古斯塔夫·基尔霍夫于 1859 年提出的传热学定律， 它用于描述物体的发射率与吸收比之间的关系。简介 一般研究辐射时采用的 黑体模型由于其吸收比等于1（α =1），而实际物体的吸收比则小于 1（1>α >0）。基尔霍夫热辐射定律则给出了实际物体的辐射出射度 与吸收比 之间的关系。M 为实际物体的辐射出射度，M b为相同温度下黑体的辐射出射度。而发射率 ε 的定义即为所以有 ε =α。所以，在热平衡条件下，物体对热辐射的吸收比恒等于同温度下的发射率。而对于漫灰体， 无论是否处在热平衡下， 物体对热辐射的吸收比都恒等于同温度下的发射率。不同层次的表达式对于定向的 光谱 ，其基尔霍夫热辐射定律表达式为对于半球空间的光谱，其基尔霍夫热辐射定律表达式为对于全波段的半球空间，其基尔霍夫热辐射定律表达式为θ 为纬度角， φ为经度角， λ 为光谱的波长， T 为温度。参考文献杨世铭，陶文铨。《传热学》。北京：高等教育出版社， 2006 年：356-379。王以铭。《量和单位规范用法辞典》。上海：上海辞书出版社普朗克黑体辐射定律普朗克定律描述的黑体辐射在不同温度下的频谱物理学中， 普朗克黑体辐射定律 （也简称作普朗克定律或黑体辐射定律）（英文：Planck's law, Blackbody radiation law）是用于描述在任意温度T 下，从一个黑体中发射的电磁辐射的辐射率与电磁辐射的频率的关系公式。这里辐射率是频率的函数[1]：这个函数在 hv=2.82kT 时达到峰值[2]。如果写成 波长的函数，在单位 立体角 内的辐射率为[3]注意这两个函数具有不同的单位：第一个函数是描述单位频率间隔内的辐射率，而第二个则是单位波长间隔内的辐射率。因而和并不等价。它们之间存在有如下关系：通过单位频率间隔和单位波长间隔之间的关系，这两个函数可以相互转换：电磁波 波长 和频率 的关系为[4]普朗克定律有时写做 能量密度 频谱的形式[5]：这是指单位频率在单位 体积 内的能量，单位是焦耳／（立方米·赫兹）。对全频域积分可得到与频率无关的能量密度。一个黑体的辐射场可以被看作是光子气体，此时的能量密度可由气体的热力学 参数决定。能量密度频谱也可写成波长的函数普朗克定律（绿）、维恩近似（蓝）和瑞利-金斯定律（红）在频域下的比较，可见维恩近似在高频区域和普朗克定律相符，瑞利-金斯定律在低频区域和普朗克定律相符...