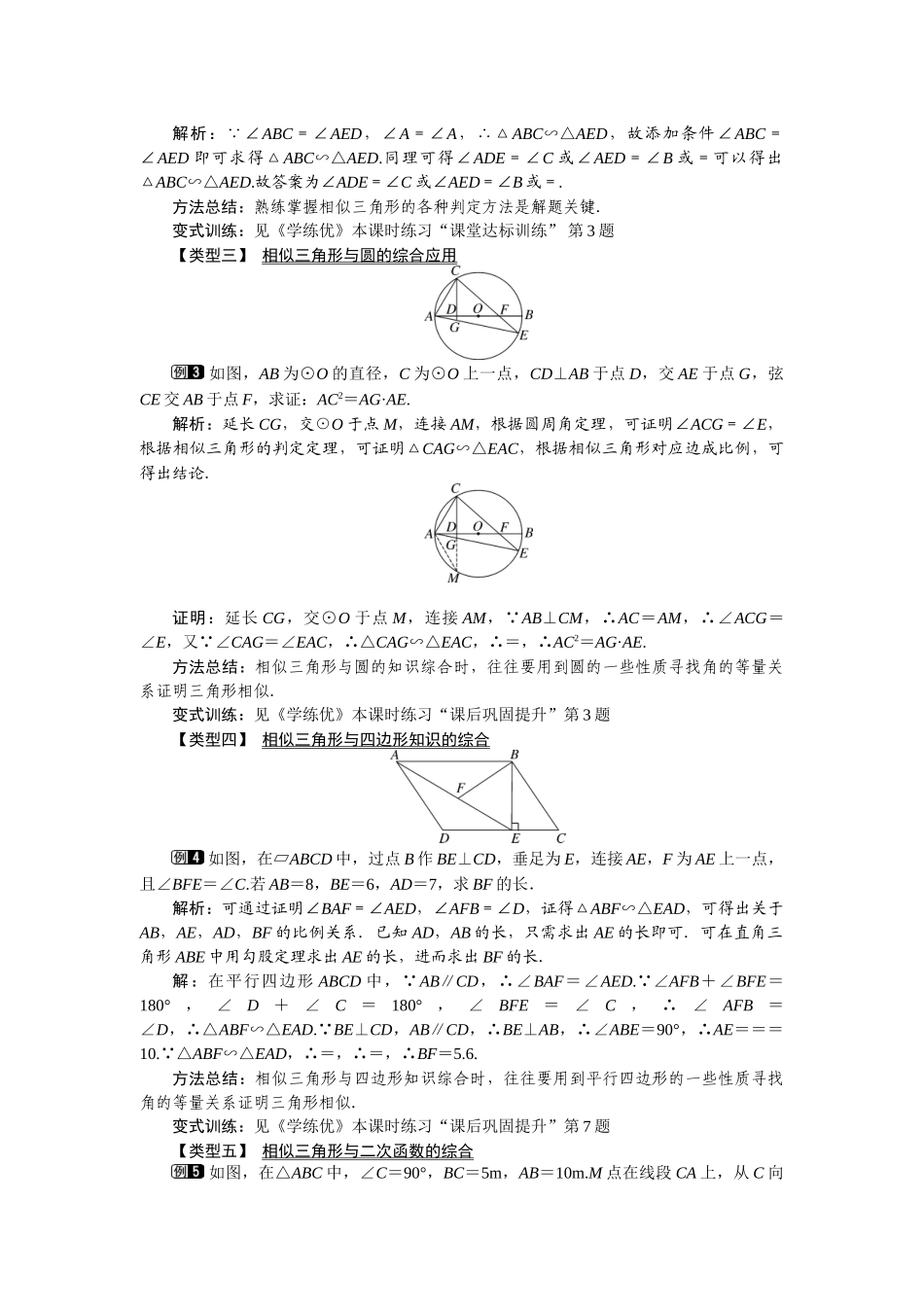
27.2.1 相似三角形的判定 第 4 课时 两角分别相等的两个三角形相似1.理解“两角分别相等的两个三角形相似”的含义,能分清条件和结论,并能用文字、图形和符号语言表示;(重点)2.会运用“两角分别相等的两个三角形相似”判定两个三角形相似,并解决简单的问题.(难点)一、情境导入与同伴合作,一人画△ABC,另一人画△A′B′C′,使得∠A 和∠A ′都等于给定的∠α,∠B 和∠B′都等于给定的∠β,比较你们画的两个三角形,∠C 与∠C′相等吗?对应边的比,,相等吗?这样的两个三角形相似吗?和同学们沟通.二、合作探究探究点:两角分别相等的两个三角形相似【类型一】 利用判定定理证明两个三角形相似 如图,在等边△ABC 中,D 为 BC 边上一点,E 为 AB 边上一点,且∠ADE=60°.(1)求证:△ABD∽△DCE;(2)若 BD=3,CE=2,求△ABC 的边长.解析:(1)由题有∠B=∠C=60°,利用三角形外角的知识得出∠BAD=∠CDE,即可证明△ABD∽△DCE;(2)根据△ABD∽△DCE,列出比例式,即可求出△ABC 的边长.(1)证明:在△ABD 中,∠ADC=∠B+∠BAD,又∠ADC=∠ADE+∠EDC,而∠B=∠ADE=60°,∴∠BAD=∠CDE.在△ABD 和△DCE 中,∠BAD=∠CDE,∠B=∠C=60°,∴△ABD∽△DCE;(2)解:设 AB=x,则 DC=x-3,由△ABD∽△DCE,∴=,∴=,∴x=9.即等边△ABC 的边长为 9.方法总结:本题主要是利用“两角分别相等的两个三角形相似”,解答此题的关键是利用三角形的外角的知识得出角相等.变式训练:见《学练优》本课时练习“课堂达标训练” 第 5 题【类型二】 添加条件证明三角形相似 如图,在△ABC 中,D 为 AB 边上的一点,要使△ABC∽△AED 成立,还需要添加一个条件为____________.解析: ∠ABC=∠AED,∠A=∠A,∴△ABC∽△AED,故添加条件∠ABC=∠AED 即可求得△ABC∽△AED.同理可得∠ADE=∠C 或∠AED=∠B 或=可以得出△ABC∽△AED.故答案为∠ADE=∠C 或∠AED=∠B 或=.方法总结:熟练掌握相似三角形的各种判定方法是解题关键.变式训练:见《学练优》本课时练习“课堂达标训练” 第 3 题【类型三】 相似三角形与圆的综合应用 如图,AB 为⊙O 的直径,C 为⊙O 上一点,CD⊥AB 于点 D,交 AE 于点 G,弦CE 交 AB 于点 F,求证:AC2=AG·AE.解析:延长 CG,交⊙O 于点 M,连接 AM,根据圆周角定理,可证明∠ACG=∠E,根据相似三角形的判定定理,可证明△CAG...