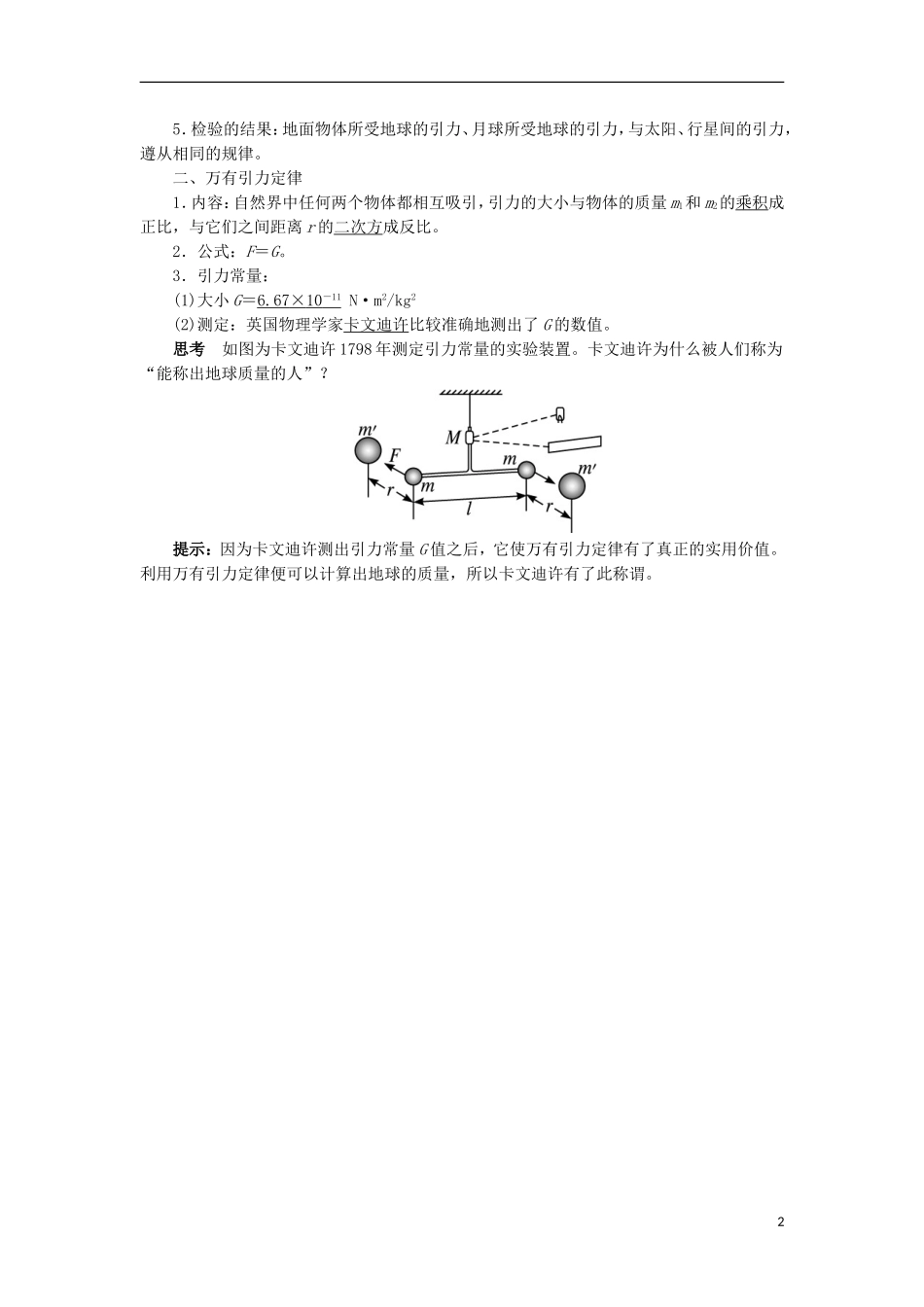
第三节 万有引力定律预习导航情境导入课程目标1.知道任何物体间都存在万有引力。2.理解万有引力定律的含义。3.知道万有引力定律表达式的适用条件,会用它进行计算。4.知道万有引力常量是自然界重要的物理常量之一。一、月—地检验1.牛顿的猜想:太阳对地球的引力、地球对月球的引力以及地球对地面上物体的引力都是同一种性质的力,遵循相同的规律。2.猜想的依据:(1)行星与太阳之间的引力使行星不能飞离太阳,物体与地球之间的引力使物体不能离开地球;(2)在离地面很高的距离内,都不会发现重力有明显的减弱,那么这个力必定延伸到很远的地方。3.检验的方法:月球轨道半径约为地球半径的 60 倍,月球轨道上物体受到的引力是地球上的。根据牛顿第二定律,物体在月球轨道上运动时的加速度(月球公转的向心加速度)应该是它在地球表面附近下落时的加速度(自由落体加速度)的。计算对比两个加速度就可以分析验证两个力是否为同一性质的力。4.检验的过程:(1)理论分析:设地球半径为 r 地,地球和月球间距离为 r 地月(2)天文观测:15.检验的结果:地面物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力,遵从相同的规律。二、万有引力定律1.内容:自然界中任何两个物体都相互吸引,引力的大小与物体的质量 m1和 m2的乘积成正比,与它们之间距离 r 的二次方成反比。2.公式:F=G。3.引力常量:(1)大小 G=6.67 × 10 - 11 N·m2/kg2(2)测定:英国物理学家卡文迪许比较准确地测出了 G 的数值。思考 如图为卡文迪许 1798 年测定引力常量的实验装置。卡文迪许为什么被人们称为“能称出地球质量的人”?提示:因为卡文迪许测出引力常量 G 值之后,它使万有引力定律有了真正的实用价值。利用万有引力定律便可以计算出地球的质量,所以卡文迪许有了此称谓。2