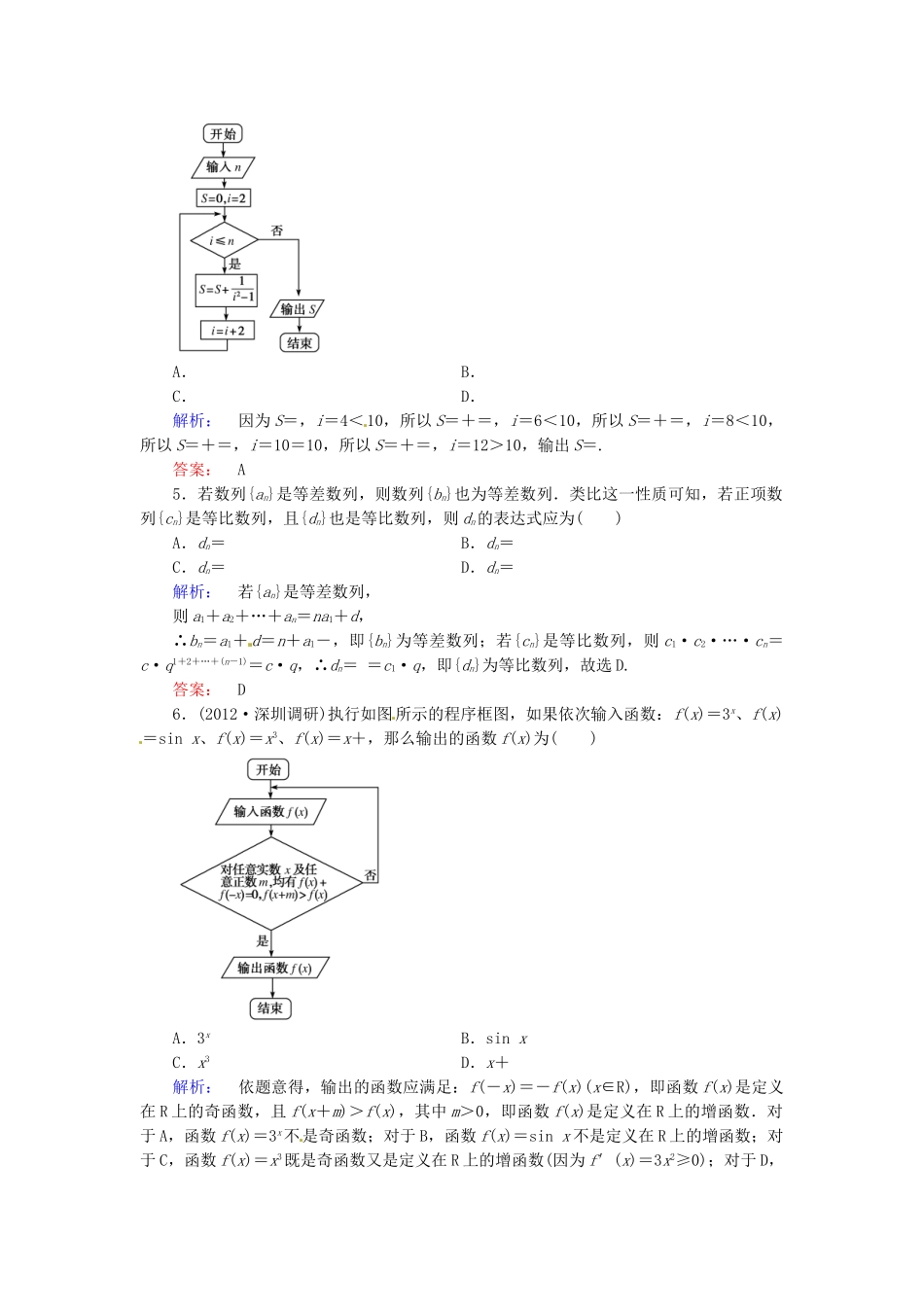
(人教专用)2014高考数学总复习热点重点难点专题透析专题3第1课时推理与证明、算法初步练习题理(本栏目内容,在学生用书中以独立形式分册装订!)1.(2013·东北三校联合考试)按如图所示的程序框图运行后,输出的结果是63,则判断框中的整数M的值是()A.5B.6C.7D.8解析:按框图所示程序运行可得S=1,A=1;S=3,A=2;S=7,A=3;S=15,A=4;S=31,A=5;S=63,A=6.此时输出S,故M为6.答案:B2.从1=1,1-4=-(1+2),1-4+9=1+2+3,1-4+9-16=-(1+2+3+4),…,归纳出()A.1-4+9-16+…+(-n)2=(-1)n-1·B.1-4+9-…+(-1)n+1·n2=(-1)n-1·C.1-4+9-…+(-1)n·n2=(-1)n-1·D.1-4+9-…+(-1)n-1·n2=(-1)n·解析:由归纳法可得B正确,故选B.答案:B3.(2013·江西卷)阅读如下程序框图,如果输出i=4,那么空白的判断框中应填入的条件是()A.S<8B.S<9C.S<10D.S<11解析:根据程序框图,i=2,S=2×2+1=5,不满足条件;i=3,S=2×3+2=8,不满足条件;i=4,S=2×4+1=9,此时输出i=4,所以填S<9.答案:B4.(2013·辽宁卷)执行如图所示的程序框图,若输入n=10,则输出S=()A.B.C.D.解析:因为S=,i=4<10,所以S=+=,i=6<10,所以S=+=,i=8<10,所以S=+=,i=10=10,所以S=+=,i=12>10,输出S=.答案:A5.若数列{an}是等差数列,则数列{bn}也为等差数列.类比这一性质可知,若正项数列{cn}是等比数列,且{dn}也是等比数列,则dn的表达式应为()A.dn=B.dn=C.dn=D.dn=解析:若{an}是等差数列,则a1+a2+…+an=na1+d,∴bn=a1+d=n+a1-,即{bn}为等差数列;若{cn}是等比数列,则c1·c2·…·cn=c·q1+2+…+(n-1)=c·q,∴dn==c1·q,即{dn}为等比数列,故选D.答案:D6.(2012·深圳调研)执行如图所示的程序框图,如果依次输入函数:f(x)=3x、f(x)=sinx、f(x)=x3、f(x)=x+,那么输出的函数f(x)为()A.3xB.sinxC.x3D.x+解析:依题意得,输出的函数应满足:f(-x)=-f(x)(x∈R),即函数f(x)是定义在R上的奇函数,且f(x+m)>f(x),其中m>0,即函数f(x)是定义在R上的增函数.对于A,函数f(x)=3x不是奇函数;对于B,函数f(x)=sinx不是定义在R上的增函数;对于C,函数f(x)=x3既是奇函数又是定义在R上的增函数(因为f′(x)=3x2≥0);对于D,函数f(x)=x+的定义域不是实数集.答案:C7.(2013·武汉市调研)如图是一个算法流程图,则输出的k的值是________.解析:根据程序框图可知,k=1时,12-1×6+5≤0;k=2时,22-2×6+5≤0;k=3时,32-3×6+5≤0;k=4时,42-4×6+5≤0;k=5时,52-5×6+5≤0;k=6时,62-6×6+5>0.故输出的k的值是6.答案:68.已知函数f(x)=,对于数列{an}有an=f(an-1)(n∈N*,且n≥2),如果a1=1,那么a2=________.an=________.解析:a2=f(a1)=,a3=f(a2)=,a4=f(a3)=,由此猜想an=.答案:9.已知命题:若数列{an}为等差数列,且am=a,an=b(m≠n,m、n∈N*),则am+n=;现已知等比数列{bn}(bn>0,n∈N*),bm=a,bn=b(m≠n,m、n∈N*),若类比上述结论,则可得到bm+n=________.解析:等差数列中的bn和am可以类比等比数列中的bn和am,等差数列中的bn-am可以类比等比数列中的,等差数列中的可以类比等比数列中的.故bm+n=.答案:10.数列{an}满足Sn=2n-an(n∈N*).(1)计算a1,a2,a3,a4,并由此猜想通项公式an;(2)用数学归纳法证明(1)中的猜想.解析:(1)当n=1时,a1=S1=2-a1,∴a1=1.当n=2时,a1+a2=S2=2×2-a2,∴a2=.当n=3时,a1+a2+a3=S3=2×3-a3,∴a3=.当n=4时,a1+a2+a3+a4=S4=2×4-a4,∴a4=.由此猜想an=(n∈N*).(2)证明:①当n=1时,a1=1,结论成立.②假设n=k(k≥1且k∈N*)时,结论成立,即ak=,那么n=k+1时,ak+1=Sk+1-Sk=2(k+1)-ak+1-2k+ak=2+ak-ak+1,∴2ak+1=2+ak,∴ak+1====,这表明n=k+1时,结论成立,由①②可知对于任意n∈N*猜想an=都成立.11.(2012·福建卷)某同学在一次研究性学习中发现,以下五个式...