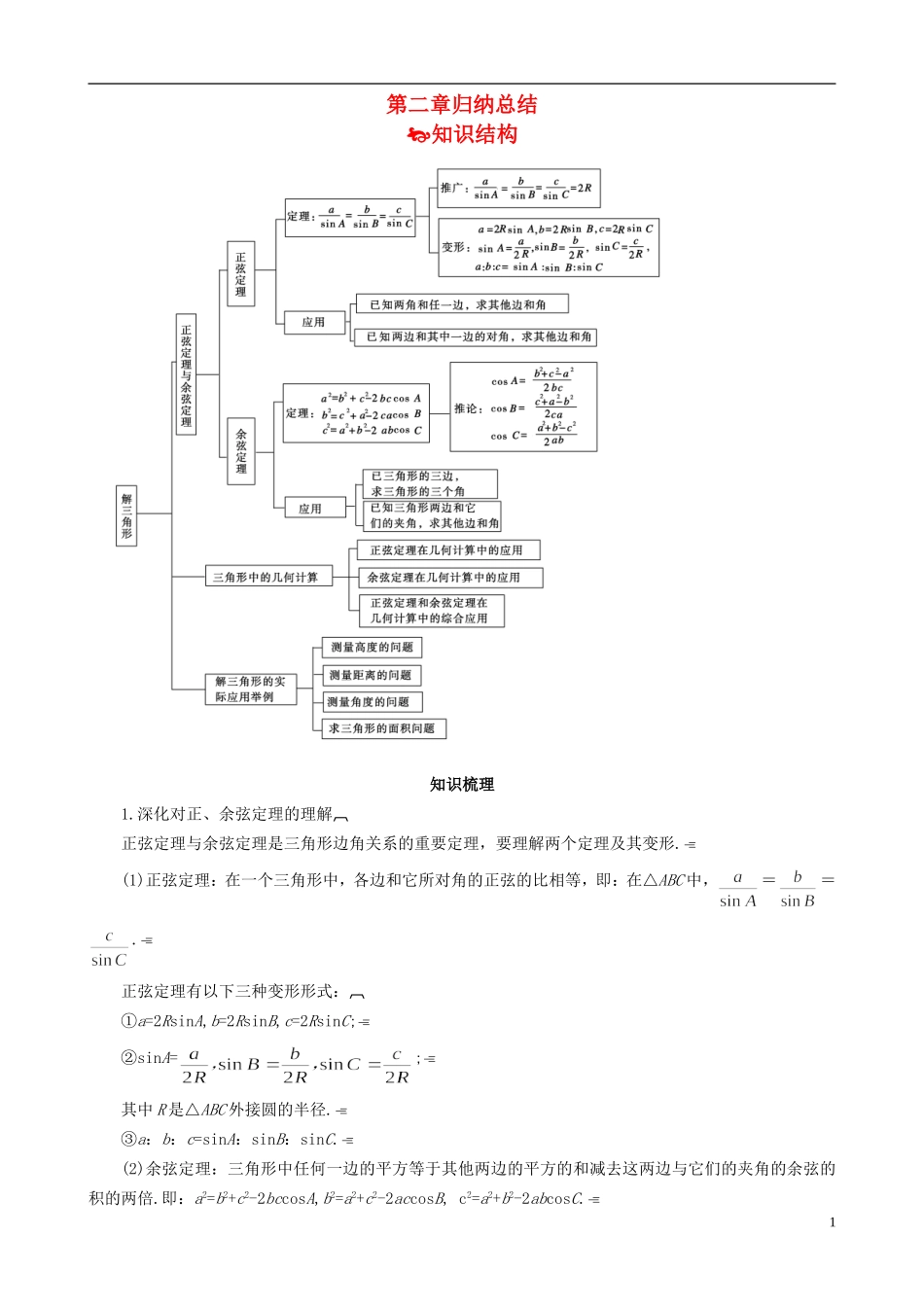
第二章归纳总结知识结构知识梳理1.深化对正、余弦定理的理解正弦定理与余弦定理是三角形边角关系的重要定理,要理解两个定理及其变形.(1)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等,即:在△ABC 中,==.正弦定理有以下三种变形形式:①a=2RsinA,b=2RsinB,c=2RsinC;②sinA=;其中 R 是△ABC 外接圆的半径.③a:b:c=sinA:sinB:sinC.(2)余弦定理:三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.即:a2=b2+c2-2bccosA,b2=a2+c2-2accosB, c2=a2+b2-2abcosC.1余弦定理的推论:cosA=,cosB=,cosC=.2.剖析斜三角形的类型与解法正弦定理、余弦定理的每一个等式中都包含三角形的四个元素(三角形有三个角和三条边,三角形的边与角称为三角形的元素),如果其中三个元素是已知的(至少要有一个元素是边),那么这个三角形一定可解.关于斜三角形的解法,根据已知条件及适用的定理,可以归纳为以下四种类型(设三角形为△ABC,A,B,C所对的边分别为 a,b,c):已知条件应用定理一般解法一边和两角(如 a,∠B,∠C)正弦定理由∠A+∠B+∠C=180°,求角 A;由正弦定理求出 b 与 c,在有解时只有一解. 两边和夹角(如 a,b,∠C)余 弦 定 理 正弦定理由余弦定理求第三边 c;由正弦定理求出一边所对的角;再由∠A+∠B+∠C=180°求出另一角,在有解时只有一解. 三边(a,b,c)余弦定理由 余 弦 定 理 求 出 角 A 、 B ; 再 利 用∠A+∠B+∠C=180°,求出角 C,在有解时只有一解. 两边和其中一边的对角(如a,b,∠A)正 弦 定 理 余弦定理由 正 弦 定 理 求 出 角 B ; 由 ∠ A +∠B+∠C=180°,求出角 C;再利用正弦定理或余弦定理求 c,可有两解、一解或无解.3.解三角形常用的边角关系及公式总结(1)三角形内角和等于 180°.(2)两边之和大于第三边,两边之差小于第三边.(3)三角形中大边对大角,小边对小角.(4)三角函数的恒等变形:sin(A+B)=sinC,cos(A+B)=-cosC,sin.(5)三角恒等变换公式,如和、差角公式,倍角公式的正用与逆用等.4.解读判断三角形形状的两种方法判断三角形的形状,应围绕三角形的边角关系进行思考,此类题目一般采用以下两种方法求解:(1)利用正弦定理化边为角,通过三角运算判断三角形的形状.(2)利用余弦定理化角为边,通过代数运算判断三角形的形状.2注意:根据余弦定理判断...