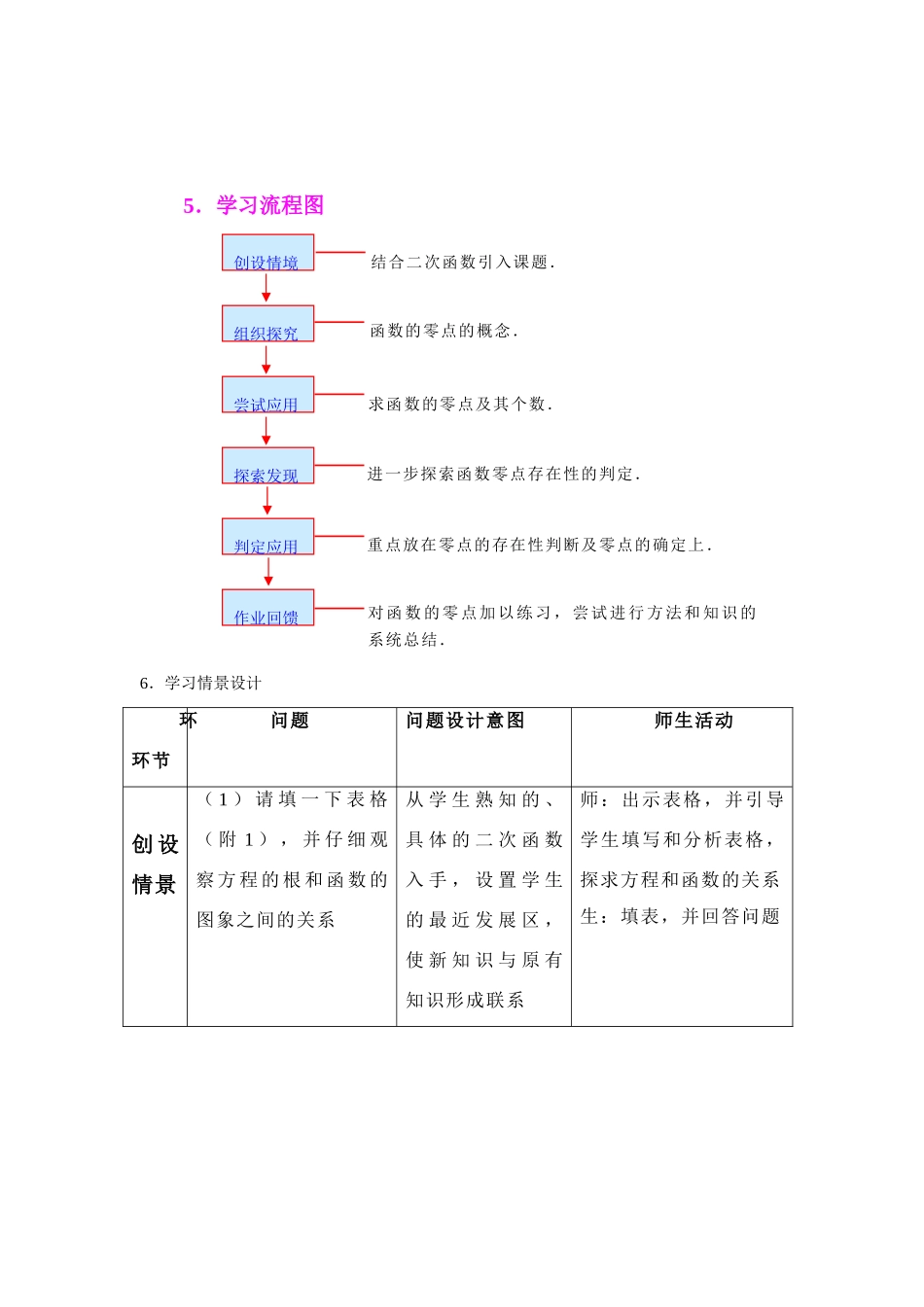
教学设计山东省莱芜市第二中学 吕汉茂 (13506342339)课题:§3.1.1 方程的根与函数的零点1.本节的地位和作用本节课是在学生对方程和函数及它们之间的关系已经有了一定的认识基础上安排的,这样安排符合学生的认知特点和学科知识的逻辑规律,使学生通过学习本节进一步体会方程与函数之间的联系;它是学习下一节“用二分法求方程的近似解”的基础,是函数的应用之一。2.学习任务分析(1)通过具体的一元二次方程和相应的函数观察出方程的根和函数的图象之间的关系,进一步将这种关系推广到一般的一元二次方程和函数,最后拓展到一般的方程和函数。(2)引出函数的零点的概念,分析出方程的根、函数的零点、函数的图象和 x 轴交点的横坐标实质上的同一性。(3)判定函数的零点可通过方程的根,也可通过函数的图象。(4)在探究由图象判定函数的零点时,找到了零点存在的判定条件。(5)通过例题的学习,进一步掌握判定函数的零点的方法,并加以归纳总结。3.学习重点和难点重点:体会函数的零点与方程的根之间的联系,掌握零点存在的判定条件难点:函数的零点存在的判定条件4.学习目标分析知识与技能 理解函数(结合二次函数)零点的概念,领会函数零点与相应方程之间的关系,掌握零点存在的判定条件过程与方法 渗透由特殊到一般的认识规律,培养学生观察、归纳、抽象和概括能力情感、态度、价值观 在函数与方程的联系中体验数学中的转化思想5.学习流程图6.学习情景设计环环节问题问题设计意图师生活动创 设情景( 1 ) 请 填 一 下 表 格( 附 1 ) , 并 仔 细 观察 方 程 的 根 和 函 数 的图象之间的关系从 学 生 熟 知 的 、具 体 的 二 次 函 数入 手 , 设 置 学 生的 最 近 发 展 区 ,使 新 知 识 与 原 有知识形成联系师:出示表格,并引导学生填写和分析表格,探求方程和函数的关系生:填表,并回答问题创设情境组织探究尝试应用探索发现判定应用作业回馈结合二次函数引入课题.函数的零点的概念.求函数的零点及其个数.进一步探索函数零点存在性的判定.重点放在零点的存在性判断及零点的确定上.对函数的零点加以练习,尝试进行方法和知识的系统总结.(2)再填一表格(附2),并分析以上关系对 一 般 的 一 元 二 次 方程 和 相 应 函 数 适 用吗?由 具 体 到 一 般 ,既 符 合 学 生 的 认知 特 点 , 又 符 合知识的发展规...