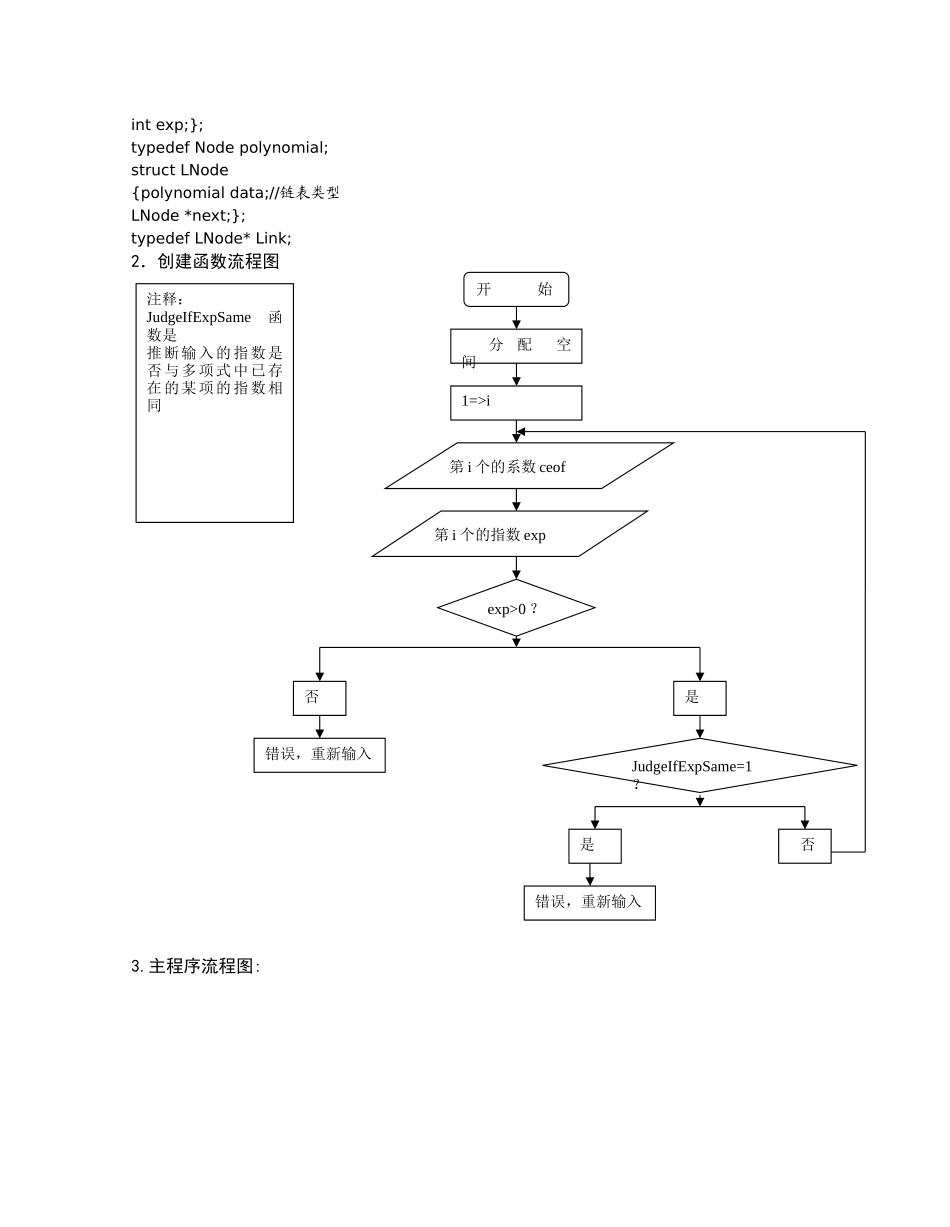
目 录1.多项式的设计报告…….………………………2 a.概要设计 …….………………………2 b.详细设计 …….………………………3 c.调试分析 …….………………………8 数据结果 …….………………………8 时间复杂度分析 ……………………10 问题和解决方法 ……………………10 源程序代码展示…………………………102.二叉树的设计报告…….………………………18 a.概要设计 …….………………………18 b.详细设计 …….………………………19 c.调试分析 …….………………………21 数据结果 …….………………………21 时间复杂度分析 ………………………22 问题和解决方法 ………………………23 源程序代码展示…………………………233.课程设计总结…………………………………26一.多项式的设计报告a. 概要设计 1. 将该存储结构定义为链式结构的线性表存储结构的定义:struct Node{float coef;//结点类型int exp;};typedef Node polynomial;struct LNode{polynomial data;//链表类型LNode *next;};typedef LNode* Link;2.创建函数流程图3.主程序流程图:开 始 分 配 空 间第 i 个的系数 ceof第 i 个的指数 expexp>0 ?否是错误,重新输入JudgeIfExpSame=1? 否是错误,重新输入1=>i注释:JudgeIfExpSame函数是推断输入的指数是否与多项式中已存在的某项的指数相同4.多项式加法的算法分析将链表 pa,pb 分别复制到新建链表 p1,p2 中,再新建链表 pc,然后分别依次对 p1,p2 链表中结点中的指数进行比较,将指数小的结点的值先赋值给 pc 中的结点,两个指数相同时,将系数相加后一起赋值给 pc 中的结点,最后将 p1 或者 p2 中多余的结点直接赋值给 pc 链表,pc 链表就是通过加法后的多项式5.多项式减法的算法分析新建链表 pt,将 pb 中的结点值赋给 pt,然后将 pt 中所有结点的系数乘上(-1)后,再将 pt 和pa 相加就得到相减后的多项式。6.多项式乘法的算法分析同样将链表 pa,pb 中的结点赋值给 p1,p2,然后依次将 p1 中的每个结点的值分别与 p2 中每个结点的值相乘后赋值给 pc,就得到相乘后的多项式。b. 详细设计一. 创建多项式的源程序void CreateLink(Link &L,int n){if(L!=NULL) //首先推断是已经存在多项式,假如存在则销毁{DestroyLink(L);}Link p,newp;L=new LNode;L->next=NULL;//分配结点空间,new 相当于 malloc ...