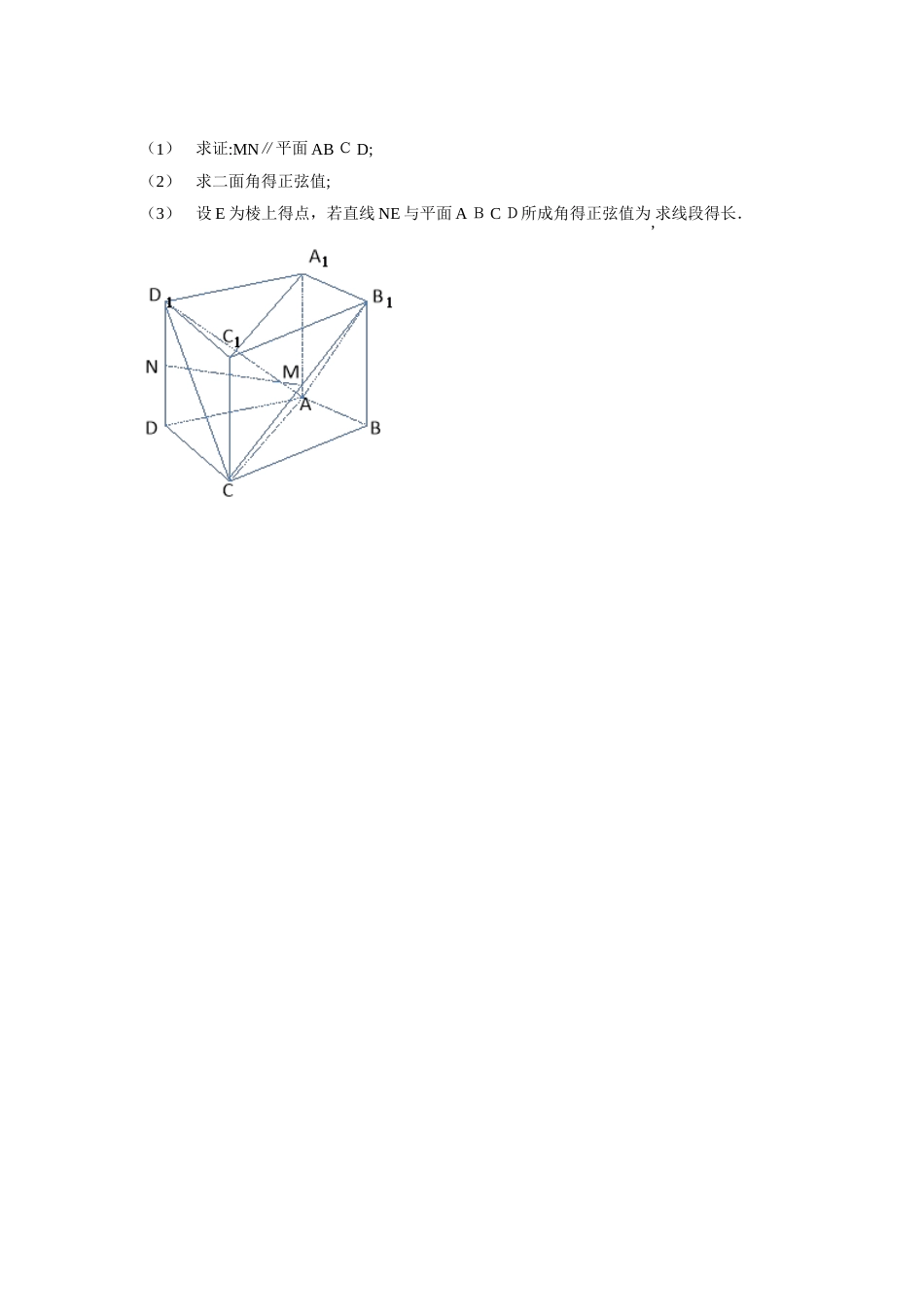
一、定义法例1 ( 如图 1 )四面体 AB C S 中,SA,SB,SC 两两垂直,∠SBA=4 5°, ∠S BC=6 0°, M 为 A B 得中点,求(1)BC 与平面 SA B所成得角。(2)SC与平面A BC 所成得角。图12、在三棱锥中,,则与平面所成角得余弦值。3、(20 16年浙江高考)如图,在三棱台 A BC-DEF 中,平面B CFE⊥平面 ABC,∠AC B=90°,BE=EF=F C=1,BC=2,A C=3、(I)求证:BF⊥平面 A C F D;(II)求直线 BD 与平面 ACFD 所成角得余弦值、4、(2 016 年天津高考)如图,四边形A BCD 就是平行四边形,平面 AE D⊥平面A BCD,EF||AB,A B=2,BC=E F=1,A E=,D E=3,∠B AD=60º,G 为 BC 得中点、(Ⅰ)求证:FG||平面 BED;(Ⅱ)求证:平面 BED⊥平面 AED;(Ⅲ)求直线 E F与平面 BED 所成角得正弦值、5、在直三棱柱中,底面就是等腰直角三角形,∠A CB=,AC=1,=,求与平面所成角得正弦值。(定义法、等体积法、向量法)二、等体积法1、如图所示得几何体中,四边形 ABCD 就是等腰梯形,AD//C D, ,FC 平面 A B CD, AE BD,CB =CD=-CF。(Ⅰ)求证:平面A BCD 平面A ED;(Ⅱ)直线 AF 与面B D F所成角得余弦值2、在如图所示得几何体中,四边形AB CD 为正方形,为等腰直角三角形,,且.(Ⅰ)证明:平面平面。(Ⅱ)求直线 E C与平面 B ED所成角得正弦值。ABCDE3、如图,已知 PA⊥平面 A B C,等腰直角三角形 ABC 中,A B=B C=2,AB⊥BC,A D⊥P B 于 D,AEPC⊥于E.(Ⅰ)求证:PCDE;⊥(Ⅱ)若直线 AB 与平面 A D E 所成角得正弦值为,求P A 得值。三、向量法1、在正方体 A B CD-得棱长为 1,求与平面所成角得正弦值.2、正三棱柱A B C-得底面边长为 2,高为,求与侧面所成得角。3、如图,在四棱锥中,∥D C,AD=D C=AP=2,A B=1,点 E 为棱 PC 得中点。(1)证明;(2)求直线 BE 与平面 P B D 所成角得正弦值;(3)若 F 为棱 P C上一点,满足,求二面角得余弦值。4、如图,在四棱柱ABCD-中,侧棱且点 M 与 N 分别为与得中点。(1)求证:MN∥平面 AB C D;(2)求二面角得正弦值;(3)设 E 为棱上得点,若直线 NE 与平面 A B C D所成角得正弦值为,求线段得长.