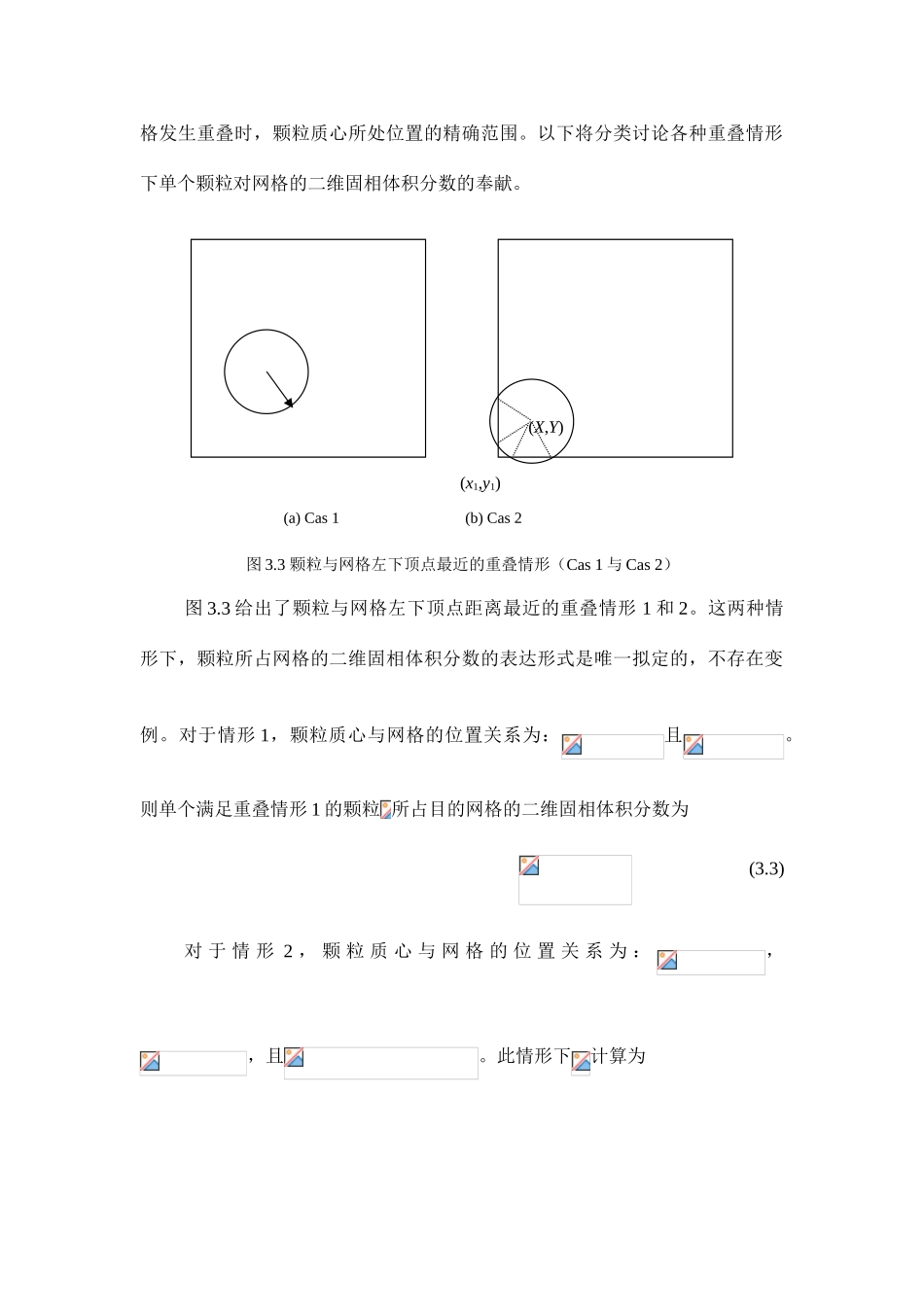
精确二维固相体积分率方案为了精确计算二维固相体积分数,将颗粒与网格的部分重叠进一步细分为四种情形。图 3.1 中给出了各种重叠情形下颗粒与网格的相对位置关系示意。计算网格的二维固相体积分数时,部分重叠的四种情形还需要进一步区分网格顶点与颗粒的位置关系。本章模拟采纳正方形网格进行空间离散,这里令颗粒的坐标为,网格宽度和厚度分别为,网格的几何中心为,网 格 的 四 个 顶 点 分 别 为,,和,由此可计算颗粒与四个顶点的距离和。这些距离中,当和分别为最小时,单颗粒所占网格的二维固相体积分数的表达形式存在差别,不失一般性,这里只给出当<,<和<同时成立时,各种重叠情形下单颗粒所占网格的二维固相体积分数的表达式。图 3.1 颗粒与控制体的五种重叠情形图 3.2 颗粒与网格重叠时颗粒质心的区域划分图 3.2 给出了当<,<和<同时成立时,各种重叠情形下颗粒质心与网格左下顶点的相对位置关系,与部分重叠的四种情形相相应,这里部分重叠时颗粒与顶点的位置关系也划分为四种情形。图 3.2 还显示了颗粒与网格发生重叠时,颗粒质心所处位置的精确范围。以下将分类讨论各种重叠情形下单个颗粒对网格的二维固相体积分数的奉献。 (a) Cas 1 (b) Cas 2图 3.3 颗粒与网格左下顶点最近的重叠情形(Cas 1 与 Cas 2)图 3.3 给出了颗粒与网格左下顶点距离最近的重叠情形 1 和 2。这两种情形下,颗粒所占网格的二维固相体积分数的表达形式是唯一拟定的,不存在变例。对于情形 1,颗粒质心与网格的位置关系为:且。则单个满足重叠情形 1 的颗粒 所占目的网格的二维固相体积分数为 (3.3) 对 于 情 形 2 , 颗 粒 质 心 与 网 格 的 位 置 关 系 为 :,,且。此情形下计算为(x1,y1)(X,Y) (3.4)图 3.4 给出了颗粒与网格左下顶点距离最近的重叠情形 3。对于情形 3,颗粒质心与网格的位置关系存在四种变例,但均满足。尽管情形 3 存在四种变例,但通过推导,颗粒所占网格的二维固相体积分数的表达形式是统一的。根据图 3.4 容易得到 (3.5) (3.6)则颗粒 所占目的网格的二维固相体积分数为 (3.7)图 3.4 颗粒与网格左下顶点最近的重叠情形(Cas 3)图 3.5 给出了颗粒与网格左下顶点距离最近的重叠情形 4。情形 4 存在两种变例,并且颗粒所占网格的二维固相体积分数的表达形式也存在差异。对于情形 4 的变例 1,颗粒质心与网格的位置关系所满足的条件为:,,...