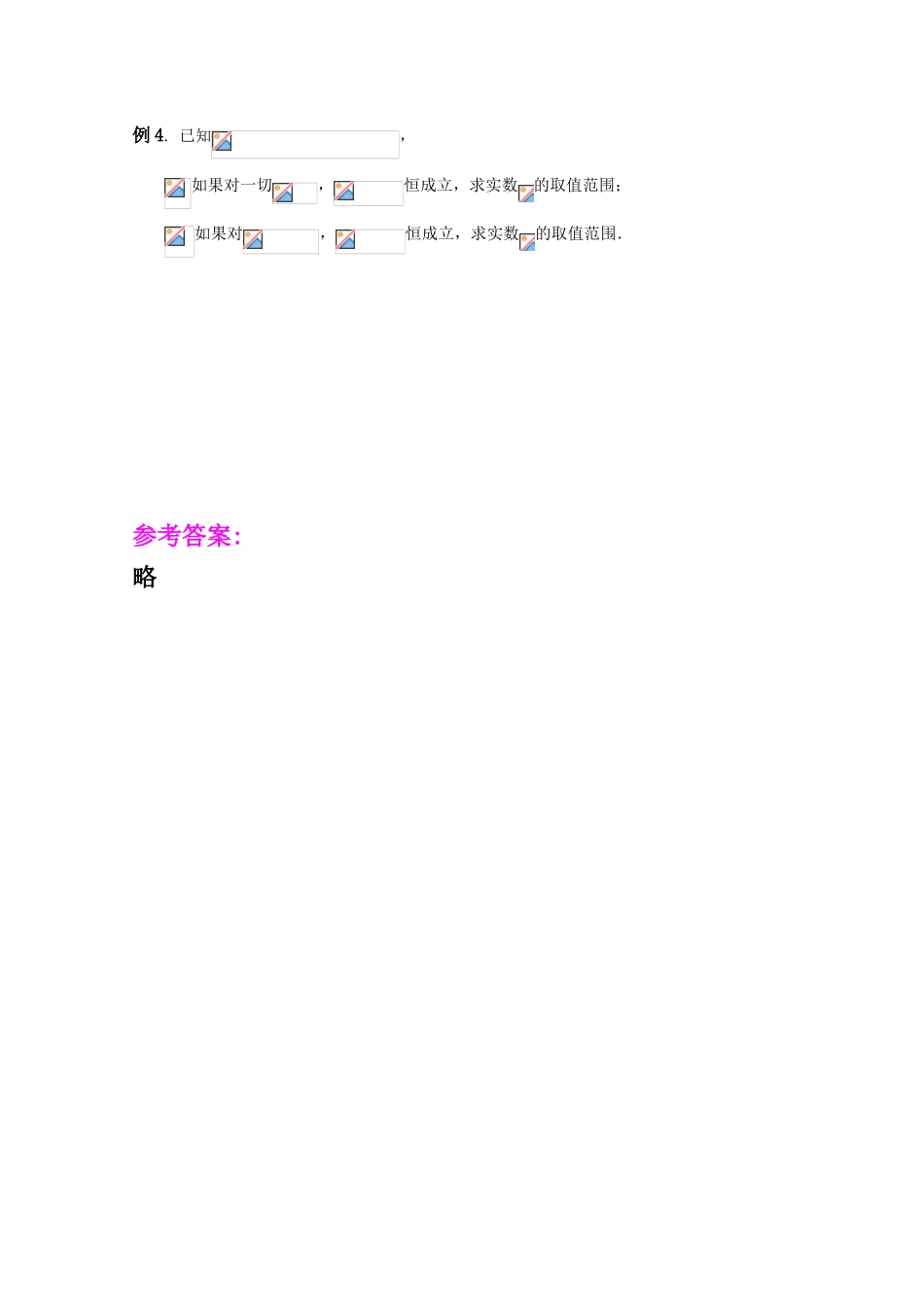
一轮复习学案 §4.2. 一元二次不等式的解法 ☆复习目标:1.掌握一元二次不等式解法,利用二次函数图象研究对应不等式解集的方法; 2.能应用一元二次不等式、对应方程、函数三者之间的关系解决综合问题; 3.会解简单的分式不等式及高次不等式.☻基础热身:1. 不等式的解集为( ) A. B. C.R D. 2. 对任意实数,不等式恒成立,则实数的取值范围是( ) A. B. C D. 3. 不等式的解集为( ) A. B. C. D. 4. 不等式的的解集为 ;的解集为 5. 若关于的不等式的解集不是空集,则实数的取值范围是 ☻知识梳理:1. 结合三个“二次”,解一元二次不等式: 10.通常先将不等式化为或的形式; 20.然后求出对应方程的根(若有根的话),再写出不等式的解: 30.大于时两根之外,小于时两根之间; ☆☆利用二次函数的图象来写出一元二次不等式的解集。 2. 分式不等式的基本解法: 通分,移项, 去括号.整理成标准型或,再用“标根引线法”. 务必注意:10.大于等于或小于等于的情况中,分母要不为零; 20.没有明确分母是正数前, 绝对不能去分母!3.高次不等式的基本解法:主要是“因式分解,标根引线” 法.4.含参数的不等式: ① 含参数的不等式要善于针对参数的取值进行讨论; ② 要善于运用“数形结合”法解决有关不等式问题; ③ 要深刻理解不等式的解集与对应方程的解之间的关系,会由解集确定参数的值. ☆案例分析:例 1. 解下列不等式:; ; ; ≥例 2. ① 二次不等式的解集是,则的值是( ) ② 已知不等式的解集为,则不等式的解集为 例 3. 下解关于的不等式:≥例 4. 已知, 如果对一切,恒成立,求实数的取值范围; 如果对,恒成立,求实数的取值范围. 参考答案:略