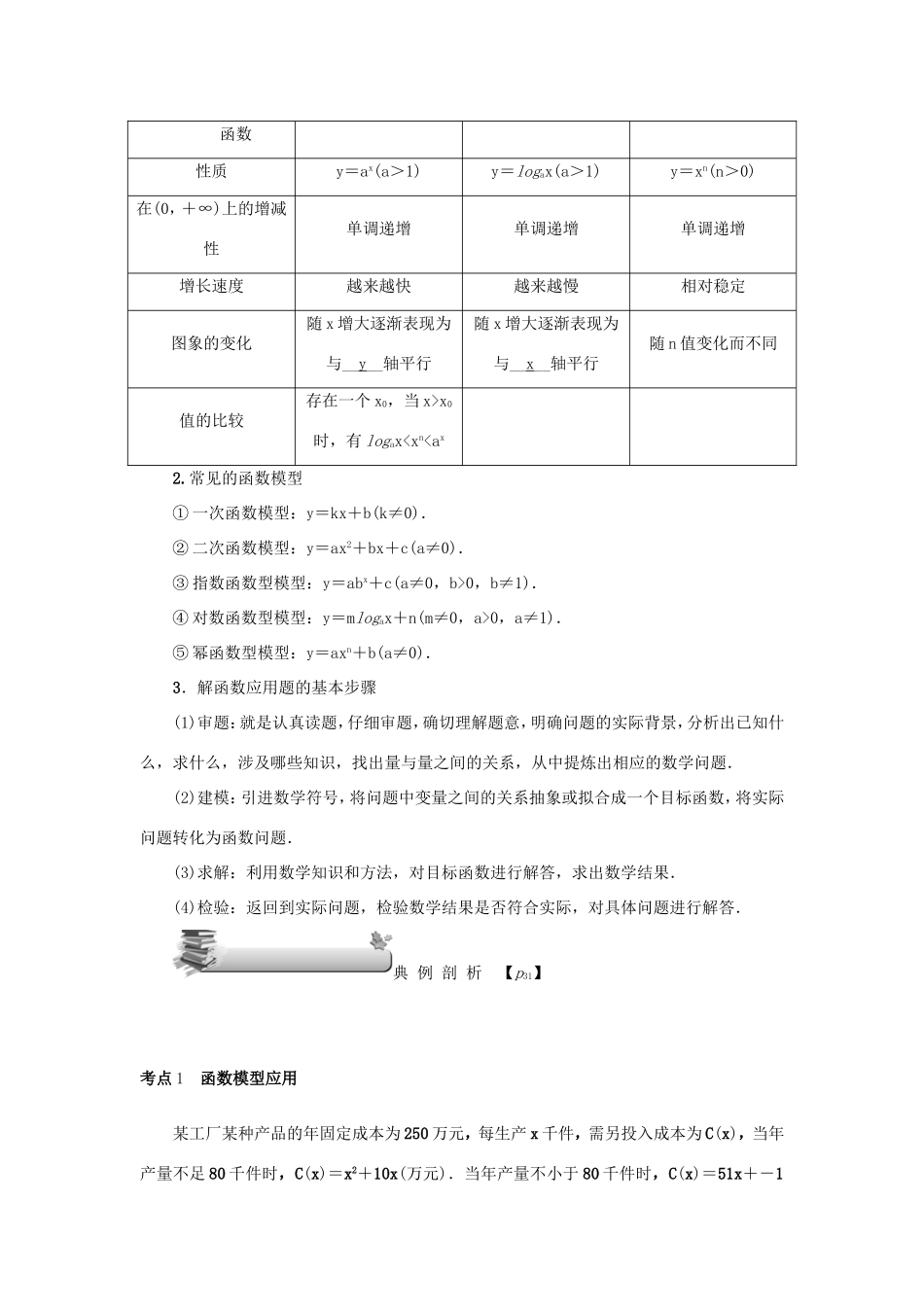
第14讲函数模型及函数的综合应用夯实基础【p31】【学习目标】1.了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同函数类型增长的含义.2.了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.3.会运用函数的知识和函数思想解决有关函数的综合性问题,培养学生分析问题和解决问题的能力.【基础检测】1.在某个物理实验中,测量得变量x和变量y的几组数据,如下表:x0.500.992.013.98y-0.990.010.982.00则对x,y最适合的拟合函数是()A.y=2xB.y=x2-1C.y=2x-2D.y=log2x【解析】根据x=0.50,y=-0.99,代入计算,可以排除A;根据x=2.01,y=0.98,代入计算,可以排除B,C;将各数据代入函数y=log2x,可知满足题意.故选D.【答案】D2.已知函数f(x)=x2,g(x)=2x,h(x)=log2x,当x∈(4,+∞)时,对这三个函数的增长速度进行比较,下列选项正确的是()A.f(x)>g(x)>h(x)B.g(x)>f(x)>h(x)C.g(x)>h(x)>f(x)D.f(x)>h(x)>g(x)【答案】B3.某电商新售A产品,售价为每件50元,年销售量为11.8万件.为支持新品发售,第一年免征营业税,第二年需征收销售额x%的营业税(即每销售100元征税x元).第二年,电商决定将A产品的售价提高元,预计年销售量减少x万件.要使第二年A产品上交的营业税不少于10万元,则x的最大值是()A.2B.5C.8D.10【解析】由题意得(11.8-x)·x%≥10,解得2≤x≤10.故选D.【答案】D4.将甲桶中的aL水缓慢注入空桶乙中,tmin后甲桶中剩余的水量符合指数衰减曲线y=aent.假设过5min后甲桶和乙桶的水量相等,若再过mmin甲桶中的水只有L,则m的值为()A.5B.8C.9D.10【解析】 5min后甲桶和乙桶的水量相等,∴函数y=f(t)=aent满足f(5)=ae5n=a,可得n=ln,∴f(t)=a·,因此,当kmin后甲桶中的水只有L时,f(k)=a·=a,即=,∴k=10,由题可知m=k-5=5.【答案】A5.pH值是水溶液的重要理化参数.若溶液中氢离子的浓度为[H+](单位:mol/L),则其pH值为-lg[H+].在标准温度和气压下,若水溶液pH=7,则溶液为中性,pH<7时为酸性,pH>7时为碱性.例如,甲溶液中氢离子浓度为0.0001mol/L,其pH值为-1g0.0001,即pH=4.已知乙溶液的pH=2,则乙溶液中氢离子浓度为______mol/L.若乙溶液中氢离子浓度是丙溶液的两千万倍,则丙溶液的酸碱性为______(填中性、酸性或碱性).【解析】由pH=2可得:-lg=2,即乙溶液中氢离子浓度为0.01mol/L;由乙溶液中氢离子浓度是丙溶液的两千万倍可得:丙溶液中氢离子浓度为=5×10-10,显然-lg>7,故丙溶液的酸碱性为碱性,故答案为0.01,碱性.【答案】0.01;碱性【知识要点】1.三种函数模型的性质函数性质y=ax(a>1)y=logax(a>1)y=xn(n>0)在(0,+∞)上的增减性单调递增单调递增单调递增增长速度越来越快越来越慢相对稳定图象的变化随x增大逐渐表现为与__y__轴平行随x增大逐渐表现为与__x__轴平行随n值变化而不同值的比较存在一个x0,当x>x0时,有logax
0,b≠1).④对数函数型模型:y=mlogax+n(m≠0,a>0,a≠1).⑤幂函数型模型:y=axn+b(a≠0).3.解函数应用题的基本步骤(1)审题:就是认真读题,仔细审题,确切理解题意,明确问题的实际背景,分析出已知什么,求什么,涉及哪些知识,找出量与量之间的关系,从中提炼出相应的数学问题.(2)建模:引进数学符号,将问题中变量之间的关系抽象或拟合成一个目标函数,将实际问题转化为函数问题.(3)求解:利用数学知识和方法,对目标函数进行解答,求出数学结果.(4)检验:返回到实际问题,检验数学结果是否符合实际,对具体问题进行解答.典例剖析【p31】考点1函数模型应用某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x),当年产量不足80千件时,C(x)=x2+10x(万元).当年产量不小于80千件时,C(x)=51x+-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(1...