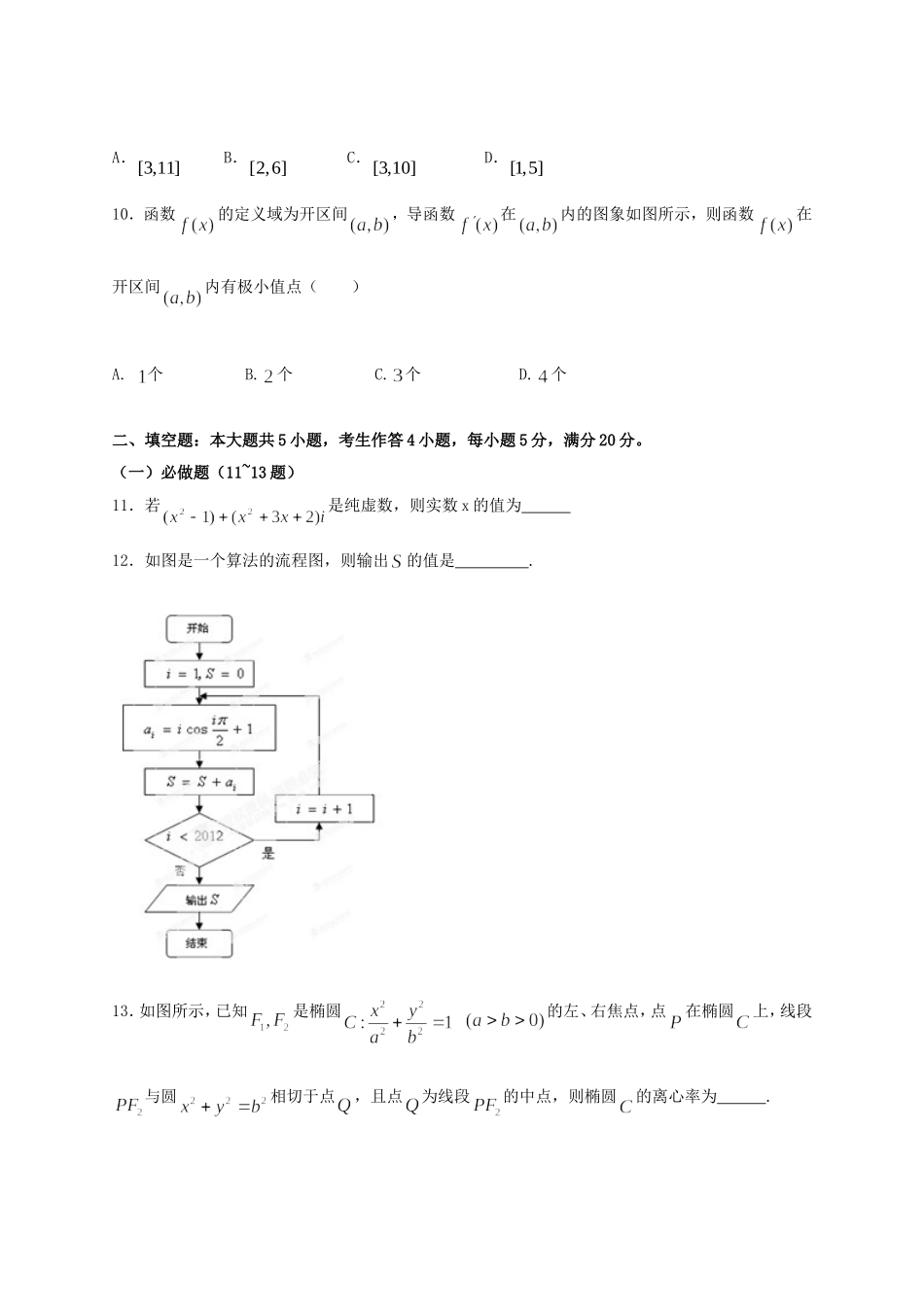
本试卷共4页,21题,满分150分。考试用时120分钟。注意事项:1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号、试室号、座位号填写在答题卡上。用2B铅笔将试卷类型(B)填涂在答题卡相应位置上。将条形码横贴在答题卡右上角“条形码粘贴处”。2.选择题每小题选出答案后,用2B铅笔把答题卡对应题目选项的答案信息点涂黑,如需改动,用橡皮擦干净后,再选涂其他答案,答案不能答在试卷上。3.非选择题必须用黑色字迹钢笔或签字笔作答,答案必须写在答题卡各题目指定区域相应位置上;如需改动,先划掉原来的答案,然后再写上新的答案;不准使用铅笔盒涂改液。不按以上要求作答的答案无效。4.作答选做题时,请先用2B铅笔填涂选做题的题号对应的信息点,再作答。漏涂、错涂、多涂的,答案无效。5.考生必须保持答题卡的整洁。考试结束后,将试卷和答题卡一并交回。一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的1.若集合,,且,则的值为()A.B.C.或D.或或2.下列说法正确的是()A.“”是“”的充要条件B.命题“”的否定是“”C.“若都是奇数,则是偶数”的逆否命题是“若不是偶数,则不都是奇数”D.若为假命题,则,均为假命题3.已知函数上是减函数,,则x的取值范围是A.B.(0,10)C.(10,+)D.4.右图是函数sin()()yAxxR在区间5[,]66上的图象.为了得到这个函数的图象,只需将sin()yxxR的图象上所有的点A.向左平移3个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变B.向左平移3个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C.向左平移6个单位长度,再把所得各点的横坐标缩短到原来的12倍,纵坐标不变D.向左平移6个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变5.关于直线、与平面、,有下列四个命题:①且,则;②且,则;③且,则;④且,则.其中假命题的序号是:()A.①、②B.③、④C.②、③D.①、④6.已知向量,满足||=2,||=3,|2+|=,则与的夹角为A.30°B.45°C.60°D.90°7.利用独立性检验来考虑两个分类变量X和Y是否有关系时,通过查阅下表来确定断言“X和Y有关系”的可信度。如果k>5.024,那么就有把握认为“X和Y有关系”的百分比为()P(k2>k)0.500.400.250.150.100.050.0250.0100.0050.001k0.4550.7081.3232.0722.7063.845.0246.6357.87910.83A.25%B.75%C.2.5%D.97.5%8.已知等比数列中有,数列是等差数列,且,则A.2B.4C.8D.169.设,xy满足约束条件04312xyxxy,则231xyx取值范围是()A.[3,11]B.[2,6]C.[3,10]D.[1,5]10.函数的定义域为开区间,导函数在内的图象如图所示,则函数在开区间内有极小值点()A.个B.个C.个D.个二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。(一)必做题(11~13题)11.若是纯虚数,则实数x的值为12.如图是一个算法的流程图,则输出的值是.13.如图所示,已知是椭圆的左、右焦点,点在椭圆上,线段与圆相切于点,且点为线段的中点,则椭圆的离心率为.(二)选做题(14-15题,考生只能从中选做一题)14.圆的圆心到直线的距离为。15.(几何证明选讲选做题)如图圆的直径,是的延长线上一点,过点作圆的切线,切点为,连接,若,则.三、解答题:本大题共6小题,满分80分。解答须写出文字说明、证明过程和演算步骤。16.(14分)设函数(其中)在处取得最大值2,其图象与轴的相邻两个交点的距离为(I)求的解析式;(7分)(II)求函数的值域。17.(12分)某校高一某班的一次数学测试成绩(满分为100分)的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:(1)求分数在[50,60)的频率及全班人数;(2)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.18.(14分)直三棱柱111CBAABC中,aBCBBAB211,90ABC,N、F分别为11CA、1...