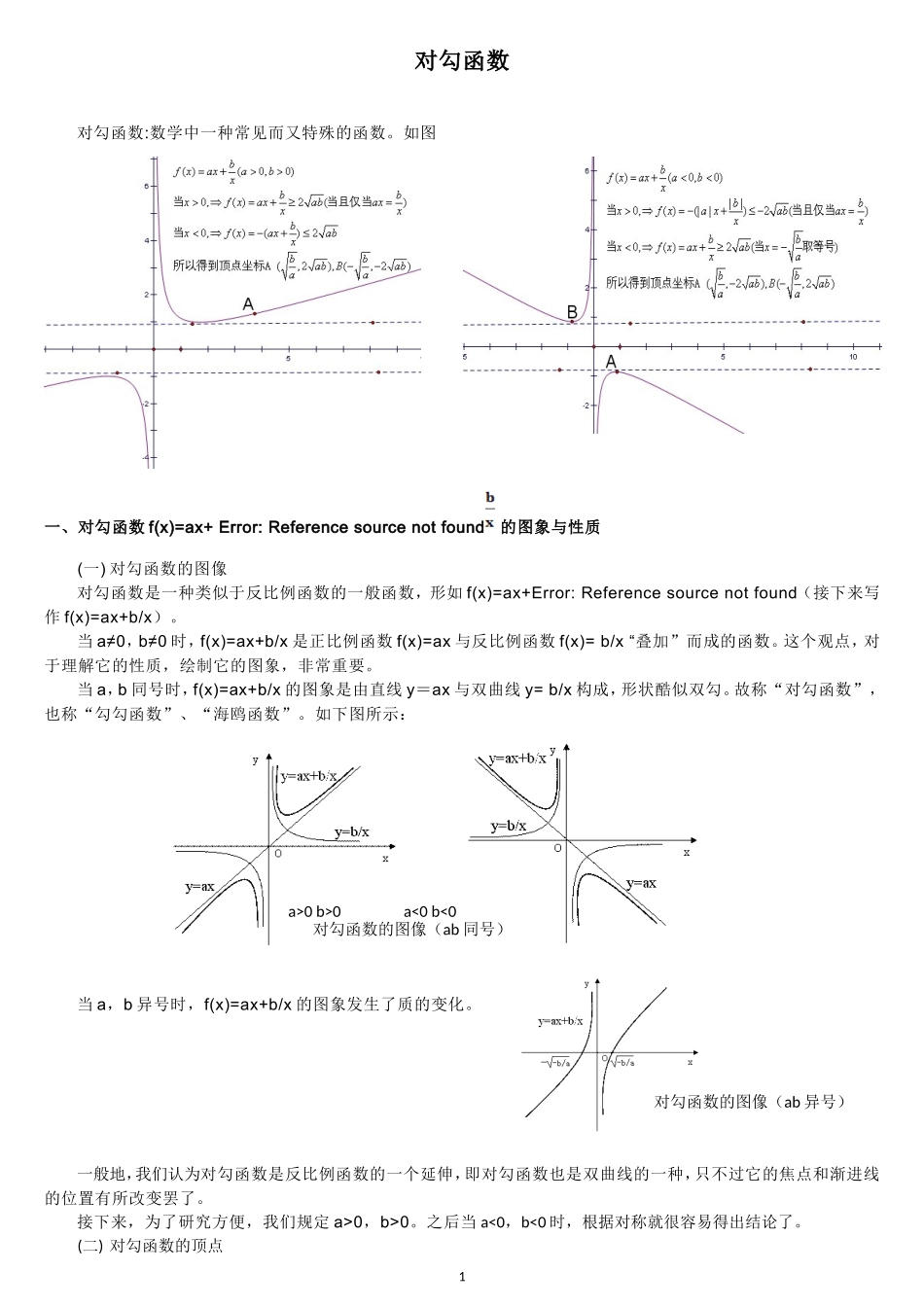
对勾函数对勾函数:数学中一种常见而又特殊的函数。如图一、对勾函数f(x)=ax+Error:Referencesourcenotfound的图象与性质(一)对勾函数的图像对勾函数是一种类似于反比例函数的一般函数,形如f(x)=ax+Error:Referencesourcenotfound(接下来写作f(x)=ax+b/x)。当a≠0,b≠0时,f(x)=ax+b/x是正比例函数f(x)=ax与反比例函数f(x)=b/x“叠加”而成的函数。这个观点,对于理解它的性质,绘制它的图象,非常重要。当a,b同号时,f(x)=ax+b/x的图象是由直线y=ax与双曲线y=b/x构成,形状酷似双勾。故称“对勾函数”,也称“勾勾函数”、“海鸥函数”。如下图所示:当a,b异号时,f(x)=ax+b/x的图象发生了质的变化。一般地,我们认为对勾函数是反比例函数的一个延伸,即对勾函数也是双曲线的一种,只不过它的焦点和渐进线的位置有所改变罢了。接下来,为了研究方便,我们规定a>0,b>0。之后当a<0,b<0时,根据对称就很容易得出结论了。(二)对勾函数的顶点1a>0b>0a<0b<0对勾函数的图像(ab同号)对勾函数的图像(ab异号)对勾函数性质的研究离不开均值不等式。利用均值不等式可以得到:当x>0时,Error:Referencesourcenotfound。当x<0时,Error:Referencesourcenotfound。即对勾函数的定点坐标:(三)对勾函数的定义域、值域由(二)得到了对勾函数的顶点坐标,从而我们也就确定了对勾函数的定义域、值域等性质。(四)对勾函数的单调性(五)对勾函数的渐进线由图像我们不难得到:(六)对勾函数的奇偶性:对勾函数在定义域内是奇函数,二、关于求函数最小值的解法1.均值不等式,,当且仅当,即的时候不等式取到“=”。当的时候,2.法若的最小值存在,则必需存在,即或(舍)找到使时,存在相应的即可。通过观察当的时候,3.单调性定义2yXOy=ax设当对于任意的,只有时,,此时单调递增;当对于任意的,只有时,,此时单调递减。当取到最小值,4.复合函数的单调性在单调递增,在单调递减;在单调递增又原函数在上单调递减;在上单调递增即当取到最小值,四、例题解析:例1、已知函数,练习:2.已知函数,求f(x)的最小值,并求此时的x值.33建筑一个容积为800米3,深8米的长方体水池(无盖).池壁,池底造价分别为a元/米2和2a元/米2.底面一边长为x米,总造价为y.写出y与x的函数式,问底面边长x为何值时总造价y最低,是多少?五、重点(窍门)其实对勾函数的一般形式是:f(x)=ax+b/x(a>0)定义域为(-∞,0)∪(0,+∞)值域为(-∞,-2√ab][2√ab,+∞∪)当x>0,有x=根号a,有最小值是2根号a当x<0,有x=-根号a,有最大值是:-2根号a对勾函数的解析式为y=x+a/x(其中a>0),它的单调性讨论如下:设x10,x1x2>0,所以f(x1)-f(x2)<0,即f(x1)0,所以f(x1)-f(x2)>0,即f(x1)>f(x2),所以函数在(-根号a,0)上是减函数⑶当00,所以f(x1)-f(x2)>0,即f(x1)>f(x2),所以函数在(0,根号a)上是减函数⑷当根号a0,x1x2>0,所以f(x1)-f(x2)<0,即f(x1)