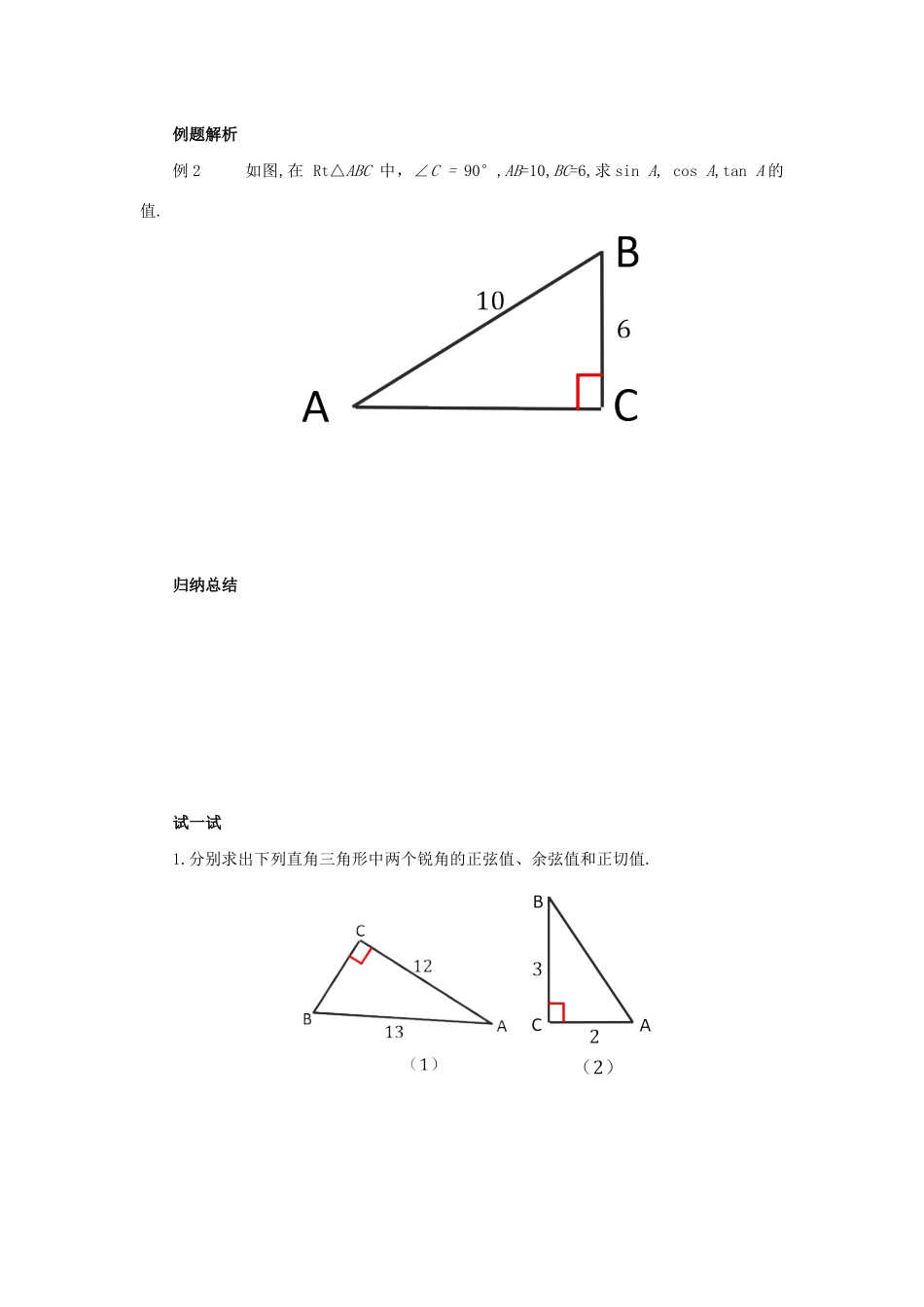
28.1锐角三角函数第2课时余弦函数和正切函数一、学习目标:1、理解余弦和正切的定义,能根据已知直角三角形的边长求一个锐角的余弦值和正切值.2、了解锐角A的三角函数的定义,能运用锐角三角函数的定义求三角函数值.二、学习重难点:重点:余弦和正切的定义难点:已知直角三角形的边长求一个锐角的余弦值和正切值.三、教学过程不能课堂导入在Rt△ABC中,∠C=90°锐角正弦的定义课堂探究知识点一:余弦函数当锐角A确定时,∠A的邻边与斜边的比,∠A的对边与邻边的比也随之确定吗?为什么?这就是我们这节课要共同学习的内容.如图,在Rt△ABC中,∠C=90°我们把锐角A的邻边与斜边的比叫做∠A的余弦,记作cosA,即cosA=¿¿例题解析例1在Rt△ABC中,∠C=90°,AB=5,BC=3,则∠A的余弦值是()A.35B.34C.45D.43归纳总结试一试1.【中考·湖州】如图,已知在Rt△ABC中,∠C=90°,AB=5,BC=3,则cosB的值是()A.35B.45C.34D.432.【中考·广东】如图,在平面直角坐标系中,点A的坐标为(4,3),那么cosα的值是()A.34B.43C.35D.45课堂探究知识点二:正切函数如图,在Rt△ABC中,∠C=90°我们把锐角A的邻边与对边的比叫做∠A的正切,记作tanA,即tanA=¿.例题解析例2如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.归纳总结试一试1.分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值.随堂检测1.已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为()A.2B.C.D.2.在△ABC中,∠C=90°,sinA=则tanB=()A.B.C.D.3.如图,小颖利用有一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是()A.B.C.D.4m4.(怀化中考)在Rt△ABC中,∠C=90°,sinA=45则cosB的值等()A.35B.45C.34D.❑√555.(东阳中考)如图,为了测量河两岸A.B两点的距离,在与AB垂直的方向点C处测得AC=a,∠ACB=α,那么AB等于()21555525434435354m23335m2335m335A.a·sinαB.a·tanαC.a·cosαD.atanα6.在Rt△ABC中,∠C=90°,AC=15,tanA=35,求AB和△ABC的面积.课堂小结1.sinA,cosA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形);2.sinA,cosA是一个完整的符号,表示∠A的正弦、余弦,习惯省去“∠”符号;3.sinA,cosA的大小只与∠A的大小有关,而与直角三角形的边长无关.我的收获__________________________________________________________________________________________________________________________________________________________参考答案课堂导入sinA=∠A的对边斜边.课堂探究知识点一:余弦函数∠A的邻边斜边=ACAB例题解析例1:C解析:在Rt△ABC中,∵∠C=90°,AB=5,BC=3,∴AC=4,∴cosA=ACAB=45.试一试1.A2.D课堂探究知识点二:正切函数∠A的对边∠A的邻边=BCAC例题解析例2解:由勾股定理得AC=❑√AB2−BC2=❑√102−62=8,因此sinA=BCAB=610=35,cosA=ACAB=810=45,tanA=BCAC=68=34.试一试(1)解:由勾股定理得BC=❑√AB2−AC2=❑√132−122=5,因此sinA=BCAB=513,sinB=ACAB=1213,cosA=ACAB=1213,cosB=BCAB=513,tanA=BCAC=512.tanB=ACBC=125.AB=❑√AC2+BC2¿❑√22+32=❑√13,所以sinA=BCAB=3❑√13=3❑√1313,sinB=ACAB=2❑√13=2❑√1313,cosA=ACAB=2❑√13=2❑√1313,cosB=BCAB=3❑√13=3❑√1313,tanA=BCAC=32.tanB=ACBC=23.(2)解:AB=❑√AC2+BC2¿❑√22+32=❑√13,所以sinA=BCAB=3❑√13=3❑√1313,sinB=ACAB=2❑√13=2❑√1313,cosA=ACAB=2❑√13=2❑√1313,cosB=BCAB=3❑√13=3❑√1313,tanA=BCAC=32.tanB=ACBC=23.随堂检测1.B2.B3.A4.B5.B6.解:∵tanA=BCAC=35,AC=15∴BC=9SΔABC=12×15×9=67.5AB=❑√AC2+BC2=❑√152+92=3❑√34